2.1 Definitionsbereich
http://www.onlinemathe.de/mathe/inhalt/Definitionsbereich
|

  
|
Übertrage die wichtigsten Informationen des folgenden Textes in dein Heft!
Der Definitionsbereich oder auch die Definitionsmenge einer Funktion f(x)
ist die Menge der Werte, die x annehmen kann.
Wollen wir den Definitionsbereich einer Funktion herausfinden, müssen wir
also die Werte ausschließen, an denen die Funktion zum Beispiel eine Polstelle hat.
Häufig ist die Definitionsmenge, die wir von nun an mit D bezeichnen, die gesamte Menge der
rationalen Zahlen R.
Haben wir jedoch eine gebrochene Funktion, in deren Nenner x enthalten ist,
so schließen wir alle x-Werte aus, mit denen der Nenner Null werden würde,
da wir nicht durch null dividieren dürfen.
Löse die Zuordnungsaufgabe:
Definitionsbereich
Wenn dir das Ganze noch nicht klar ist, benutz den Link, um nochmal nachzulesen, was ein Definitionsbereich ist.
Lernstoff
|
2.2 Stetigkeit
http://www.mathematik.de/ger/fragenantworten/erstehilfe/stetigkeit/stetigkeit.html
|

 

|
Übertrage die wichtigsten Informationen des folgenden Textes in dein Heft!
Stetig heißt im gewönlichen Sprachgebrauch nicht sprunghaft. Auch mathematische Funktionen werden stetig genannt, wenn es zu keinen plötzlichen Veränderungen der Funktionswerte kommt.
Genauer wird definiert:
Eine in einem offenem Intervall um x0 definierte Funktion y = f(x) heißt an der Stelle x0 stetig wenn gilt:
- der Grenzwert der Funktion an der Stelle x0 existiert und
- dieser Grenzwert mit dem Funktionswert übereinstimmt: limx->x0 f(x) = f(x0).
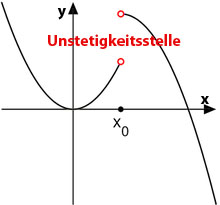
Trifft auch nur eine der beiden Bedingungen nicht zu, so heißt die Funktion an x0 unstetig.
Ist die Funktion an jeder Stelle ihres Definitionsbereiches stetig, so wird sie als stetige Funktion bezeichnet.
Löse das Multiple-Choice-Quiz:
Stetigkeit
Um noch genauer zu verstehen, was Stetigkeit ist und wie man diese überprüfen kann, sieh dir auch den Link an.
Lernstoff
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



