5.1 Extrema
http://www.onlinemathe.de/mathe/inhalt/Extrema
|

 

|
Eine Funktion y = f(x) besitzt an einer Stelle x0 ein lokales Maximum f(x0) bzw. ein lokales Minimum f(x0), wenn für alle x ≠ x0 in einer Umgebung von x0 gilt:
f(x0) > f(x) bzw. f(x0) < f(x)
x0 heißt Maximums- bzw. Minimumsstelle, allgemein eine Extremalstelle bzw. Extremum.
Maximum bzw. Minimum werden auch als Hochpunkt bzw. Tiefpunkt
bezeichnet.
Ein Extremum kann auch global sein, wenn sich die Extremaleigenschaft auf den gesamten Definitionsbereich bezieht. Globale Extrema können auch am Rand des Definitionsbereiches auftreten.
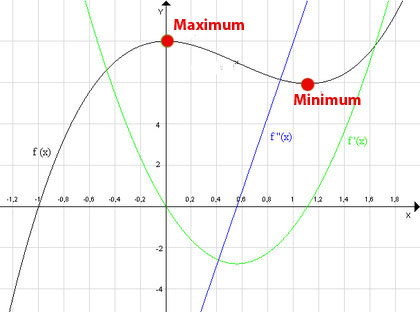
Hat eine Funktion an einer Stelle x0 ein lokales Extremum und ist sie dort differenzierbar, so ist anschaulich verständlich, dass ihr Graph an der Stelle x0 eine waagrechte Tangente besitzt.
Das heißt die Funktion besitzt dort eine Ableitung mit dem Wert 0.
Wenn du noch nicht verstehst, was Extrema sind, sieh dir den Link an!
Lernstoff
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



