|
1.1 Definition und Eigenschaften
|

 
|
Exponentialfunktionen sind Funktionen, die durch eine Funktionsgleichung y = ax ( a ∈ ℝ+\{1} ) dargestellt werden k�nnen. Die unabh�ngige Variable x tritt somit als Exponent einer konstanten, positiven Basis ungleich 1 auf.
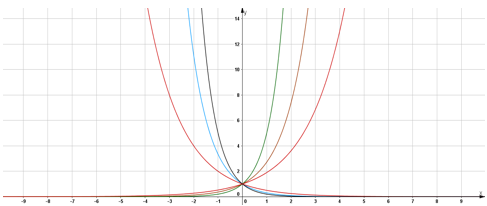
Nun möchten wir einige Eigenschaften dieser Funktionen betrachten:
- Die Definitionsmenge ist: D = ℝ
- Die Wertemenge ist: W = ℝ+
- Die x-Achse ist Asymptote
- x → ax geht immer durch den Punkt P(0|1)
- x → ax ist streng monoton wachsend für a>1
- x → ax ist streng monoton fallen für a<1
- ist die Basis a > 1, so gilt: der Funktionsgraph ist umso steiler, je größer a ist
- ist die Basis a < 1, so gilt: der Funktionsgraph ist umso steiler, je kleiner a ist
- x → ax und x → a-x liegen symmetrisch bezüglich der y-Achse
Versuche, ob du die Eigenschaften der Exponentialfunktionen wiedererkennen kannst!
Reguliere hierzu den Schieberegler für die Basis a der Exponentialfunktion in der
GeoGebra-Datei !
Lernstoff, Übungsaufgabe
|
|
1.2 Übungen
|

 

|
Aufgabe 1) Zeichne die Graphen folgender durch ihre Funktionsgleichung gegebenen Funktionen für x ∈ [-2;3] in dein Heft:
a) y = 3x
b) y = 3-x
c) y = 3|x|
d) y = 1/(3|x|)
Überprüfe anschließend deine Darstellung, indem du die Graphen noch einmal mit GeoGebra im gegebenen Intervall zeichnest, drucke die Plots aus und klebe sie unter deine selbst gezeichneten in das Heft!
Aufgabe 2) Plotte die Graphen folgender durch ihre Funktionsgleichung gegebener Funktionen im Intervall [-3;3] mit GeoGebra! Was fällt dir dabei auf? In welchem Zusammenhang stehen die Graphen? Überprüfe die Eigenschaften von Exponentialfunktionen (siehe 1.1) anhand dieses Beispiels!
a) y = 4x
b) y = 4-x
c) y = 4|x|
d) y = 1/(4|x|)
Übungsaufgaben
|
|
1.3 Die Eulersche Zahl
|

 
|
Die Eulersche Zahl e ist irrational, d.h. sie kann nicht durch einen Bruch dargestellt werden. Des Weiteren kann sie auch nicht durch die n-te Wurzel (n ∈ ℕ) einer rationalen Zahl dargestellt werden. Somit sagen wir: e ist eine transzendent irrationale Zahl. Sie nimmt etwa einen Wert von 2,71828 (gerundet!, kann als irrationale Zahl auch keine periodische Dezimalzahl sein!) ein und ist in diesem Kapitel von besonderer Bedeutung, da man mit ihrer Hilfe viele Naturgesetze, Zusammenhänge und Abhängigkeiten beschreiben kann.
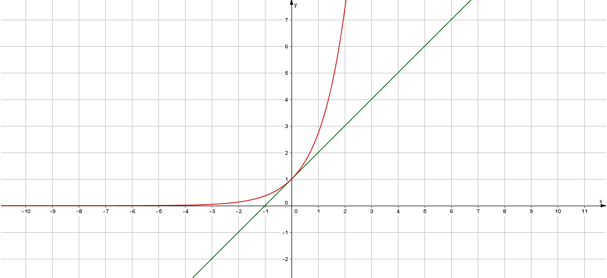
Für die Exponentialfunktion mit Basis e gilt: ex ≥ 1+x , somit verläuft die Kurve von ex (bis auf den Punkt in dem sich die beiden Graphen schneiden- Welcher ist hier wohl gemeint?) stets über der von f(x) = 1 + x .
Hiermit ist gemeint: Egal welchen Wert (mit Ausnahme von 0 → im Punkt P(0|1) schneiden sich die Funktionsgraphen und nehmen somit denselben Wert an) man für x einsetzt, ex ist immer größer als 1 + x.
Die Eulersche Zahl wurde nach dem Schweizer Mathematiker Leonhard Euler (1707-1783) benannt. Das Verzeichnis seiner Werke umfasst rund 900 Titel.
Er stammte aus einer Pastorenfamilie in Basel und studierte beim bekannten Naturwissenschaftler Johann Bernoulli (1667-1748). Von 1727-1741 war er an der Petersburger Akademie der Wissenschaften, von 1741-1766 an der von Friedrich dem Großen gegründeten Berliner Akademie und ab 1766 wieder in Petersburg tätig.
Außer mit zahlreichen Gebieten der Mathematik beschäftigte sich Leonhard Euler unter anderem mit Philosophie, Schiffsbau, Artilerie, Astronomie, Kartografie, Optik und Musiktheorie. Beispielsweise berechnete er für Friedrich den Großen Lotterien und konstruierte Brunnen mit Wasserspielen für den Schlosspark von Sanssouci (Potsdam).
1738 verlor er nach einer schweren Infektion das Sehvermögen des rechten Auges und erkrankte 1771 auch am linken Auge schwer, sodass er in den letzten Jahren seines Lebens beinahe blind war.
Er ist noch heute für sein unfehlbares Gedächtnis und seine enorme Konzentrationsfähigkeit bekannt. Seine Lehrbücher prägten den noch heute üblichen Stil!

Vertiefung
|
|
1.4 Anwendung
|

 
|
Die Bedeutung der Exponentialfunktionen liegt vor allem im Bereich der Naturwissenschaften und der Wirtschaft.
Mit ihrer Hilfe können Wachstums- und Abnahmeprozesse beschrieben werden: Zinseszinsen, Bevölkerungs- und Pflanzenwachstum,
radioaktiver Zerfall von Atomkernen, Erwärmungs- und Abkühlungsprozesse, etc.
Gemäß einer Exponentialfunktion vermehrt sich z.B. die Menschheit oder der Holzbestand eines Waldes.
Bei Abnahmeprozessen wird oft die Halbwertszeit τ betrachtet. Dies ist die Zeit, nach der noch die Hälfte der Ausgangsmenge, Ausgangsanzahl, etc. (N0) vorhanden ist - also N(τ) = N0/2.
Mache nun die folgenden Beispiele im nächsten Unterkapitel (1.4 Beispiele zur Anwendung von Exponentialfunktionen) !
Vertiefung
|
|
1.5 Beispiele zur Anwendung von Exponentialfunktionen
|

 

|
Aufgabe 1) Eine Bakterienkultur besteht zum Zeitpunkt t = 0 Stunden aus N0 = 1000 Individuen, die sich stündlich durch Zellteilung verdoppeln.
a) Wie lautet jene Funktionsgleichung N = N(t), welche den Wachstumsprozess beschreibt?
b) Fertige für t = 0, 1, 2, 3 Stunden eine Wertetabelle an und zeichne diese Werte (auf der x-Achse die Zeit in Stunden, auf der y-Achse die dazugehörige Bakterienanzahl N(t))in ein Koordinatensystem ein! Wie sieht der Funktionsgraph aus, der N(t) (zu einem beliebigen Zeitpunkt t) darstellt?
c) Auf welche Anzahl ist die Bakterienkultur nach Ablauf einer halben Stunde angewachsen?
Tipp: Bei a) Zum Zeitpunkt t = 0 existieren N0 = 1000 Bakterien, das bedeutet N(0) = 1000.
Dadurch, dass sich die Bakterienzahl stündlich verdoppelt, weißt du auch, wie viele Bakterien, es zum Zeitpunkt 1 Stunde (N(1)) gibt.
Dasselbe gilt nun auch für den Zeitpunkt t = 2, t = 3, usw. Kannst du nun allgemein sagen, wie viele Bakterien es nach t Stunden gibt? Die gesuchte Exponentialfunktion ist von der Form
N(t) = N0 ∗ at. Welche Basis besitzt die gesuchte Funktion?
Aufgabe 2) Nährstoffreiche Substanzen und feuchte Wärme von 20°C bis 37°C stellen günstige Lebensbedingungen für Bakterien dar (z.B. Bakterien des Zahnbelags). Dabei vermehren sich diese durch Zweiteilung etwa nach τ = 20 min. Man untersuche, wie viele Lebewesen sich aus einer Bakterienzelle bei ungeänderten Umweltbedingungen innerhalb eines Tages bilden können. Die Vermehrung durch Zweiteilung führt auf folgende exponentielle Abhängigkeit: A(t) = A0 ∗ 2t/τ, wobei A0 die Bakterienanzahl nach 0 min ist. Betrachte in unserem Beispiel A0 = 1, da wir ja wissen wollen, wie viele Bakterien sich eben genau aus einer Zelle nach einem Tag bilden können.
Aufgabe 3) In einem TR = 22°C warmen Zimmer liegt ein Grippekranker mit einer Körpertemperatur von TK = 38,5°C. Er benutzt ein Fieberthermometer, dessen Prüfspitze sich nach dem folgenden Gesetz erwärmt:
T = TK - (TK - TR) ∗ e(-t/τ) , mit τ = 1,5 min, t in min, T in °C
Auf welche Temperatur T ist das Thermometer nach 10 min angestiegen?
Aufgabe 4) Bei der embryonalen Entwicklung teilen sich die vorhandenen Zellen zunächst unabhängig voneinander. Die Anzahl z der Zellen wächst dann nach dem Gesetz z = 2t, wobei t die Anzahl der Teilungsperioden ist. Dieses Exponentialgesetz gilt aber nur bis etwa zur achten Teilungsperiode. Danach verändert sich der Teilungsprozess und man kann nicht mehr von einem exponentiellen Wachstum sprechen.
Wie groß ist die Anzahl der Zellen nach jeder Teilungsperiode (t = 1,....,8)?
Aufgabe 5) Der Luftdruck p nimmt mit zunehmender Höhe (über dem Meeresspiegel) ab und zwar nach der Formel p = p0 ∗ e-0,13h (p in bar, h in km, p0 = 1,013 bar auf Meereshöhe, 1mbar = 1hPa)
Wie groß sind demnach die durchschnittlichen Luftdruckwerte an folgenden geografischen Orten?
a) Graz (Steiermark) auf 353 m
b) Großglockner (Kärnten, Osttirol) auf 3797 m
c) Turracher Höhe (Kärnten, Steiermark) auf 1783 m
d) Wien auf 171 m
e) Mt. Everest (Nepal) auf 8848 m
Übungsaufgaben
|
1.6 Zunahme oder Abnahme?
http://www.mathe-online.at/tests/log/zunabn.html
|

 
 

|
Handelt es sich bei den gegebenen Termen jeweils um Wachstums- oder Abnahmeprozesse? Löse die Aufgabe und zeige, was du schon gelernt hast! ☺
Falls dir dies noch etwas schwer fällt, lies noch einmal nach, wie man eine solche Aufgabe lösen könnte! Die Funktionen mit GeoGebra darzustellen, kann ebenfalls eine große Hilfe sein!
Selfchecking Test
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



