|
2.1 Wiederholung: Logarithmus - Definition und Erklärung
|

 
|
Jene Zahl x ∈ ℝ, für die ax = b (a ∈ ℝ+\{1},b ∈ ℝ+) gilt, heißt Logarithmus von b zur Basis a:
ax = b ⇔ x = logab = logaax
Nun wirst du dich bestimmt fragen: WOZU braucht man das jetzt und was soll das überhaupt heißen??
Nun ja, stell dir vor, du möchtest wissen, wie groß x ist, wenn 3x = 9 gilt. Hier wirst du wahrscheinlich schnell erkennen: x = 2. Wie kannst du aber nun x berechnen, wenn du beispielsweise weißt, dass 3x = 5 ist?
Durch Probieren kannst du zumindest das Intervall, in dem x liegen muss, einschränken:
1 < x < 2, da 31 = 3 und 32 = 9
1,4 < x < 1,5 da 31,4 = 4,65554 und 31,5 = 5,19615
1,42 < x < 1,48 da 31,42 = 4,75896 und 31,48 = 5,08323
usw.
Bezeichnungen: In x = logab heißt:
a Basis
b Numerus
x Logarithmus
Den Logarithmus berechnen, bedeutet den Exponenten einer Potenz bestimmen.
Von besonderer Bedeutung sind Logarithmen zur Basis 10. Man nennt sie dekadische Logarithmen, Zehnerlogarithmen oder Briggsche Logarithmen.
Auch Logarithmen zur Basis e sind sehr wichtig! Sie heißen natürliche Logarithmen und statt logea schreibt man oft ln(a) ("Logarithmus naturalis"). Hiermit gilt: ln(e) = 1.
Früher benutzte man zur Berechnung von Logarithmen "Logarithmentafeln", heute besitzt jeder Taschenrechner eine "Logarithmustaste".
Wiederholung
|
|
2.2 Übungen
|

 

|
Aufgabe 1) Berechne folgende Logarithmen zur gegebenen Basis:
a) log39
b) log464
c) log7(1/49)
d) log0,5(1/32)
Aufgabe 2) Berechne x:
a) log2x = 10
b) logx125 = 3
c) x = ln(0,2)
d) ln(x) = 5
Übungsaufgaben
|
|
2.3 Wiederholung: Rechengesetze für Logarithmen
|

 

|
Für u > 0, v > 0, a > 0, a ≠ 1, r ∈ ℝ n ∈ ℕ\{0} gilt:
1) loga(u ∗ v) = logau + logav
2) loga(u/v) = logau - logav
3) loga(ur) = r ∗ logau
4) loga(u(1/n)) = (1/n) ∗ logau
Vereinfache zur Wiederholung folgende Terme so weit wie möglich:
a) log(abcd)
b) log(a4-b4)3
c) log((ab)/(cd))
d) 2∗loga-3∗logb+5∗logc
Wiederholung, Übungsaufgaben
|
|
2.4 Logarithmusfunktionen- Definition und Eigenschaften
|

 
|
Logarithmusfunktionen sind Funktionen, die durch eine Funktionsgleichung y = logax (a ∈ ℝ+\{1}, x ∈ ℝ+) dargestellt werden können.
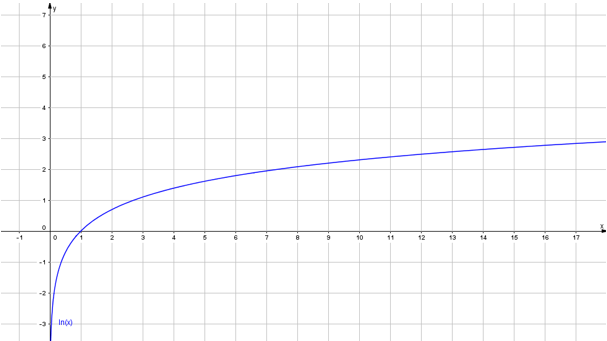
Einige Eigenschaften der Funktion x → logax:
- Definitionsmenge: D = ℝ+
- Wertemenge: W = ℝ
- Die y-Achse ist Asymptote.
- geht immer durch den Punkt P(1|0)
- ist für a>1 streng monoton wachsend, für 0 < a < 1 streng monoton fallend
- ist die Umkehrfunktion von x → ax
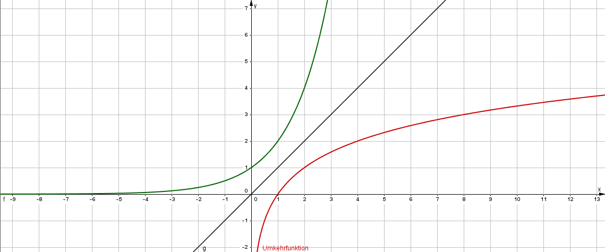
Um dir diese Eigenschaften zu veranschaulichen, ruf folgenden Link auf und ändere die Basis mit Hilfe des Schiebereglers!
Lernstoff, Übungsaufgabe
|
|
2.5 Übungen
|

 

|
Aufgabe 1) Gib die Umkehrfunktion der durch ihre Funktionsgleichung gegebenen Funktion an!
a) y = 2x
b) y = 2-x
Aufgabe 2) Stelle die logarithmische Funktion grafisch mithilfe von GeoGebra dar! Wie sieht die Umkehrfunktion dieser Funktion aus? Spiegle den Graphen der gegebenen Funktion an der 1.Mediane!
y = ln(3x)
Aufgabe 3) Löse folgende Gleichungen mit Hilfe von GeoGebra! Speichere deine Lösung als Datei ab! Wie arbeitet GeoGebra, um sie zu lösen? Gib den Lösungsweg bei einer der Gleichungen im CAS-Feld als Text an!
a) 3x=272
b) 21-x = 64
c) 9x+3 = 1/27
d) 23x-3 ∗ 42x+2 ∗ 8x+1 = 16
Aufgabe 4) Löse folgende Gleichungen mithilfe von GeoGebra! Gib die Lösungsmenge in ℝ an! Speichere deine Lösung als Datei ab! Wie könnte GeoGebra bei der Lösung solcher Gleichungen vorgehen? Beschreibe den Lösungsvorgang einer der Gleichungen als Text im CAS-Feld!
a) log10(x5) - log10(x2) = log10(8)
b) ln(3x-5) + ln(15-8x) = ln(6x-11) + ln(7-4x)
Übungsaufgaben
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



