|
2.1 Was ist ein Punkt? Was ist ein Vektor?
|

 

|
Schon seit Jahrhunderten versuchten Mathematiker zu erläutern was denn nun eigentlich ein Punkt ist.

Quelle: https://homepages-fb.thm.de/boergens/marken/03_12/euklid.pdf
In der Koordinatengeometrie bezeichnen wir einen Punkt als eine exakte Ortsangabe.
Ein Vektor besitzt eine Länge und eine Richtung.
Ein Ortsvektor zum Beispiel beschreibt die Position eines Punktes ausgehend vom Urpsurng (0,0,0).
Die Länge des Ortsvektors beschreibt in diesem Fall den Abstand des Punktes zum Ursprung
Lernstoff
|
|
2.2 Rechnen mit Vektoren
|

 

|
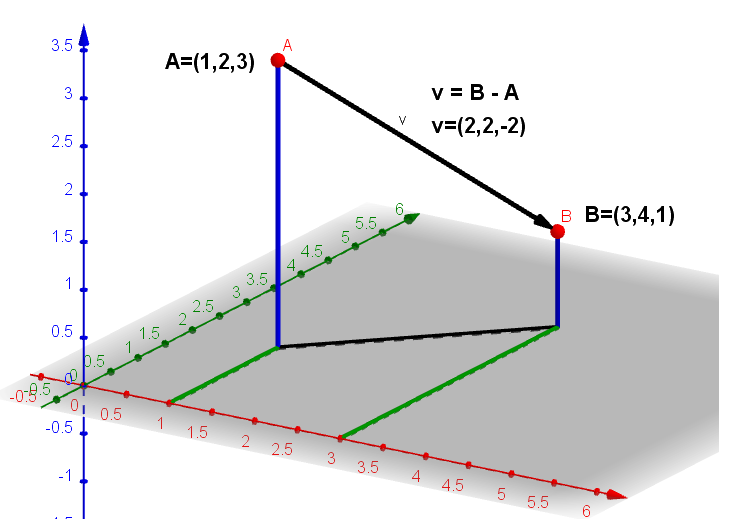
Den Verbindungsvektor zwischen zwei Punkten wird durch die Subtraktion der jeweiligen Koordinaten erreicht.
Sei A = (xA, yA, zA) und B = (xB, yB, zB)
Dann ist der Verbindungsvektor v
v = ( xB - xA, yB - yA, zB - zA )
Bestimme den Verbindungsvektor der folgenden Punkte!
P = (-2, 6, 1) und Q = (1, 3, 4)
M = (4, -1, -1) und N = (-2, 1, -1)
L = (7, -2, 4) und J = (7, 2, -4)
Übungsaufgabe
|
|
2.3 Richtungsvektoren
|

 

|
Nun beschreiben Vektoren nicht nur Punkte und Abstände, sondern auch Richtungen.
Hierbei ist jedoch wichtig, dass verschieden Vektoren die gleiche Richtung beschreiben können.
Zum Beispiel beschreiben die Vektoren
v = (1, 0, 0) und u = (3, 0, 0)
beide die Richtung der x - Achse.
Sie unterscheiden sich lediglich in ihrer länge.
Im allgemeinen sagt man, wenn zwei Vektoren linear abhängig sind, beschreiben sie die gleich Richtung.
Zwei Vektoren werden als linear abhängig bezeichnet wenn folgendes gilt:
Für v = (xv, yv, zv) und u = (xu, yu, zu) existiert ein M
sodass
M*xv = xu
M*yv = yu
M*zv = zu
Ein Beispiel:
p = (-3, 2, 4) und q = (6, -4, -8)
Diese beiden Vektoren sind linear abhängig da eine solche Zahl existiert:
(-2)*p = q
3 Vektoren a, b, c nennt man linear unabhängig falls zwei Zahlen M, N existieren sodass
M*a + N*b = c
a und b sind hierbei nicht notwendigerweise linear abhängig.
Sind a und b linear unabhängig, a, b, und c jedoch linear abhängig, dann liegt der Vektor c in der Ebene, welche von den Vektoren a und b aufgespannt wird.
Überprüfe bei den folgenden Vektoren ob sie die gleiche Richtung beschreiben!
a = (-2, 5, 4) und b = (-3, 6, 5)
u = (4, 2, -6) und v = (2, 1, -3)
n = (-1, 4, -4) und m = (0, 3, -3)
p = (3, 5, -2) und q = (-3, -5, 2)
Übungsaufgabe
|
|
2.4 Norm eines Vektors
|

 

|
Die Norm eines Vektors beschreibt dessen Länge.
Die Norm eines Ortsvektors eines Punktes beschreibt zum Beispiel den Abstand des Punktes zum Ursprung.
Der Verbindungsvektor zweier Punkte beschreibt hingegen den Abstand dieser zwei Punkte.
Die Allgemeine Formel lautet:
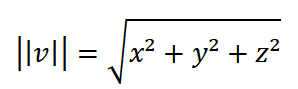
Die Berechnung der Norm lässt sich auf den Satz des Pythagoras zurückführen.
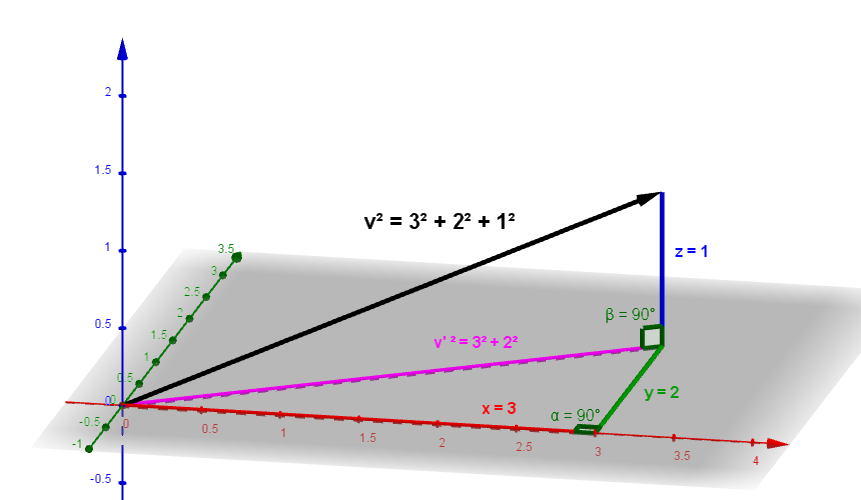
In diesem Beispiel beträgt die Länge des Vektors v somit ca. 3.75 Längeneinheiten.
Berechne die Normen der folgenden Vektoren!
u = (2, 0 ,3)
p = (5, -2, -3)
q = (0, 0, 4)
Übungsaufgabe
|
|
2.5 Normalvektor
|

 

|
Wie wir in der Ebene einen Normalvektor finden wissen wir bereits.
Im Raum ist dies jedoch etwas schwierig, da es auf einen Vektor im Raum unendlich viele Normalvektoren gibt.
Zwei lineare unabhängige Vektoren hingegen haben einen eindeutigen Normalvektor.
Dieser wird mithilfe des Kreuzproduktes gebildet.
Sei a = (a1, a2, a3) und b = (b1, b2, b3)
dann wird das Kreuzprodukt gebildet druch:
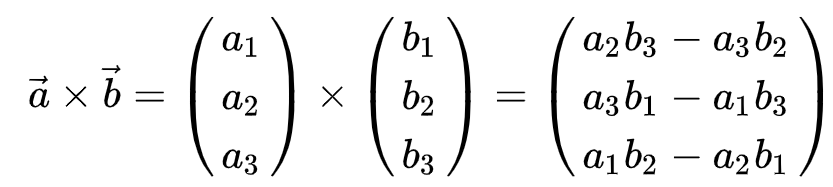
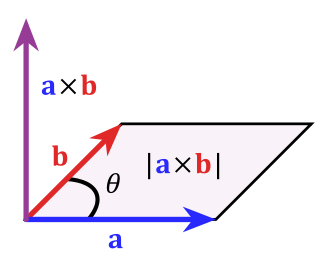
(Quelle: https://de.wikipedia.org/wiki/Kreuzprodukt)
Die Norm des Kreuzproduktes zweier Vektoren beschreibt den Flächeninhalt des Parallelogramms, welches durch die beiden Vektoren erzeugt wird.
Sind die Vektoren linear abhängig existiert kein eindeutiger Normalvektor und man erhält den Nullvektor (0, 0, 0)
Bestimme den Normalvektor der folgenden Vektorenpaare!
u = (3, -1, 2) und v = (2, 2, -1)
a = (-2, 4, 8) und b = (1, -2, -4)
p = (-3, 2, 5) und q = (-1, -1, 2)
Übungsaufgabe
|
|
2.6 Das Skalarprodukt
|

 

|
Das Skalarprodukt (oder auch inneres Produkt genannt) zweier Vektoren weißt diesen beiden Vektoren ein Skalar zu.
Man kann das Skalarprodukt als die Länge der Normalprojektion des ersten Vektors auf den zweiten verstehen. Oft auch als "Schatten" beschrieben.
Folglich lässt sich schließen, dass das Skalarprodukt zwei orthogonaler Vektoren null sein muss.
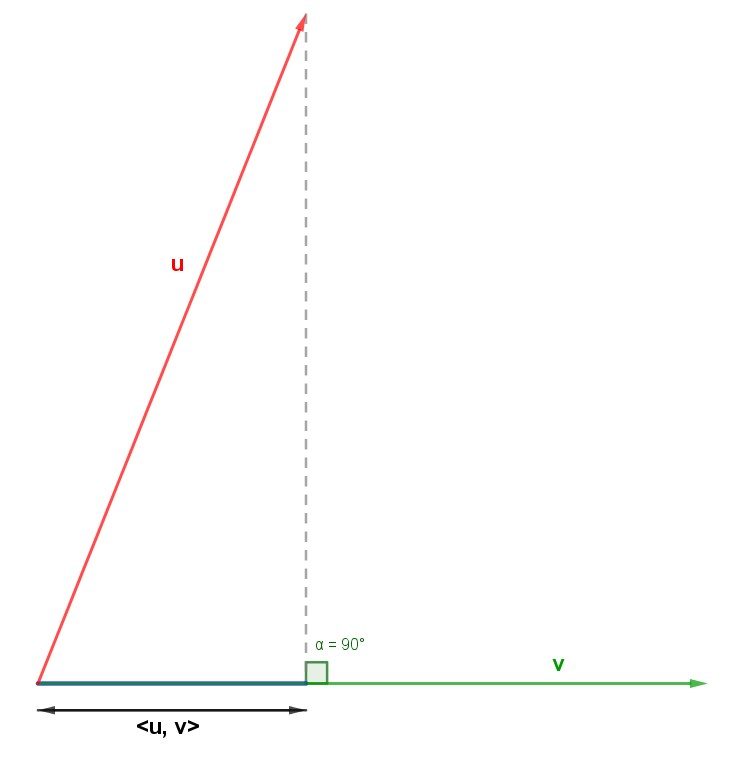
Das Skalarprodukt berechnet sich durch Multiplikation der jeweiligen Koordinaten, welche anschließend addiert werden.
Sei v = (xv, yv, zv) und u = (xu, yu, zu)
dann lautet das Skalarprodukt
<v,u> = (xv * xu) + (yv * yu) + (zv * zu)
Lernstoff
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



