Wir betrachten folgendes Gleichungssystem:
    I:  x + y = 4
   II: 4x - 2y = 4

(1)
Zuerst formt man beide Gleichungen nach y um:

   I:  x + y = 4
       ->  y = -x + 4

   II: 4x - 2y = 4
          - 2y = -4x + 4
       ->    y = 2x - 2

Beide Gleichungen haben nun die Form y = kx + d
Wie du dich bestimmt erinnern kannst, ist eine Gleichung dieser Form eine Geradengleichung! 
Solltest du dich doch nicht mehr erinnern, lies in deinem Schulbuch/-heft nach oder
informiere dich unter auf mathe-online zum Thema Geradengleichungen! 

Nennen wir die Gerade der ersten Gleichung g1: y = -x + 4
und die Gerade der zweiten Gleichung g2: y = 2x - 2

(2)
Zeichnen wir nun die beiden Geraden in ein Koordinatensystem:


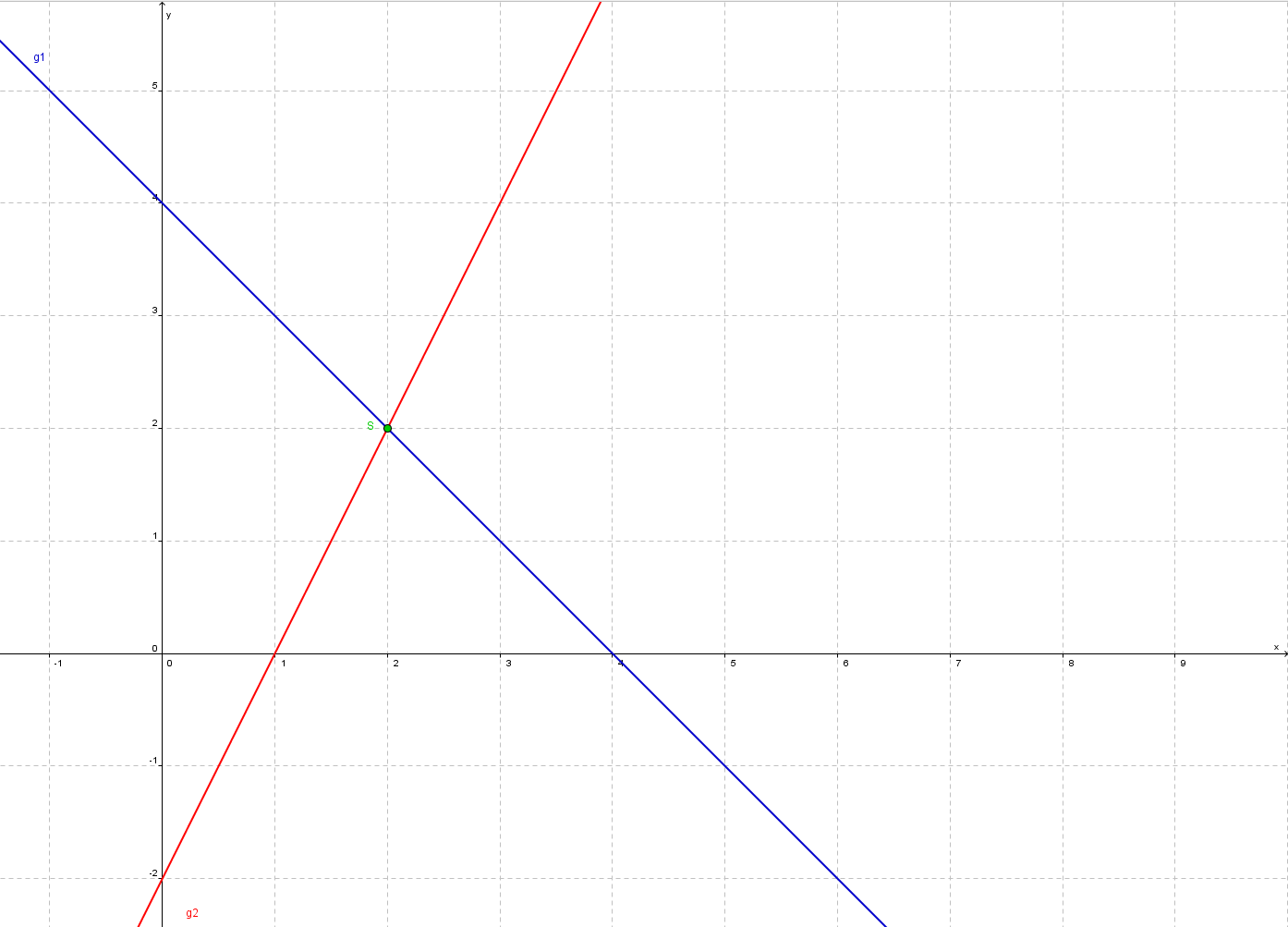(3)
Um das Gleichungssystem zu lösen, suchen wir ein Zahlenpaar (x|y), das sowohl die erste
als auch die zweite Gleichung erfüllt! 
Oder anders ausgedrückt: Wir suchen einen Punkt (x|y), der sowohl auf g1 als auch auf g2 liegt!
Und das ist genau der Schnittpunkt der beiden Geraden!

In unserem Beispiel können wir von der Zeichnung ablesen, dass der Schnittpunkt der 
Geraden g1 und g2 die Koordinaten (2|2) hat. Somit besteht die Lösungsmenge des
Gleichungssystems aus dem Punkt (2|2).
Man schreibt: L = {(2|2)}


  

    

Folgerung:
Um ein Gleichungssystem mit zwei Variablen grafisch zu lösen, braucht man nur die beiden
Geraden in ein Koordinatensystem zu zeichnen und miteinander zu schneiden!
Der Schnittpunkt ist die Lösung des Gleichungssystems!


  


     

Wie du in der Wiederholung gesehen hast, müssen sich zwei Geraden nicht immer in
einem Punkt schneiden! Wie wirkt sich diese Tatsache nun auf die Lösungsmenge eines
Gleichungssystems aus?

Sehen wir uns 2 Beispiele an:

Beispiel 1:

    I:  2x + y = 1   -> y = -2x + 1
   II: 2x + y = 3   -> y = -2x + 3

Wir zeichnen die beiden Geraden in ein Gleichungssystem:


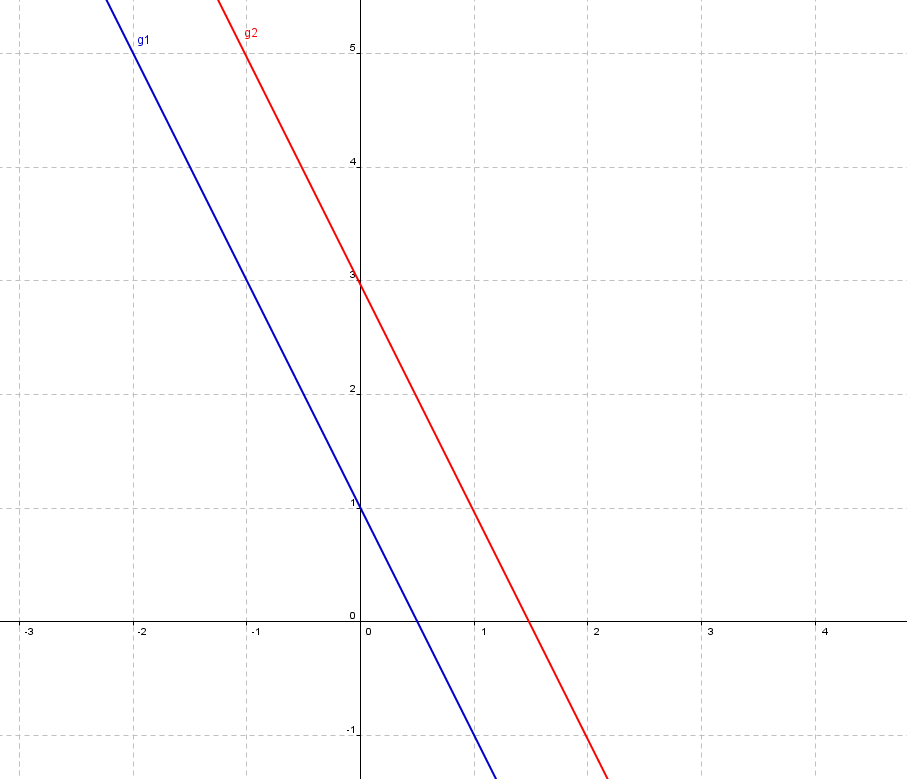Aufgrund der Gleichungen und der Grafik erkennen wir, dass die beiden Geraden parallel sind! 
Das bedeutet, sie haben keinen Punkt gemeinsam! 
Für unser Gleichungssystem bedeutet das: Es gibt kein Zahlenpaar (x|y), das
sowohl die erste, als auch die zweite Gleichung erfüllt! Die Lösungsmenge ist also leer!
Man schreibt: L = {}


Beispiel 2:

    I:  2x - y = 2    -> y = 2x - 2
   II: 4x - 2y = 4   -> y = 2x - 2

Wir zeichnen die beiden Geraden in ein Gleichungssystem:


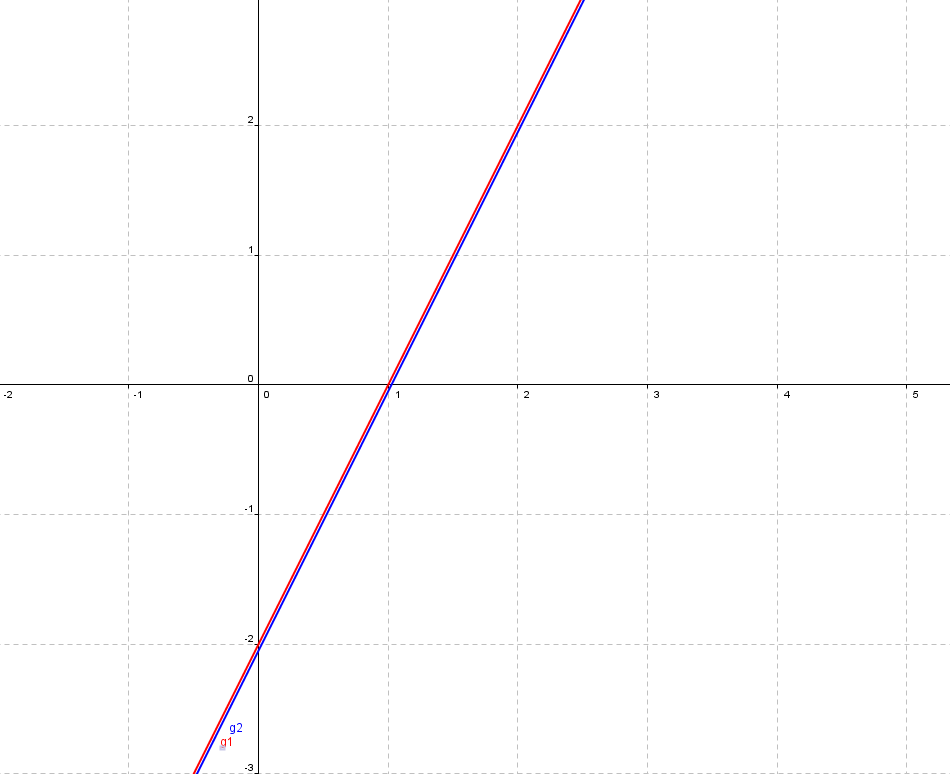Aufgrund der Gleichungen und der Grafik erkennen wir, dass die beiden Geraden identisch sind! 
Das heißt, dass sie in jedem Punkt übereinstimmen! 
Für dieses Gleichungssystem bedeutet das: Es gibt unendlich viele
Zahlenpaare (x|y), die beide Gleichungen erfüllen! Und zwar sind das genau diese
Punkte, die auf der Geraden y = 2x - 2 liegen! Das bedeutet, die Lösungsmenge ist die Menge aller 
Punkte, die auf der Geraden liegen!
Man schreibt: L = {(x|y) | y = 2x - 2}



  

    

Folgerung:
Für ein lineares Gleichungssystem mit 2 Variablen gibt es 3 Lösungsmöglichkeiten:
1. Die beiden Geraden schneiden sich => Es gibt genau eine Lösung
2. Die beiden Geraden sind parallel => Es gibt keine Lösungen
3. Die beiden Geraden sind identisch => Es gibt unendlich viele Lösungen


  

Überprüfe dein Wissen über die unterschiedlichen Lösungsmöglichkeiten 
eines linearen Gleichungssystems mit 2 Variablen!