Die Lösungsmenge eines linearen Gleichungssystems in 2 Variablen lässt sich mit der 
grafischen Lösungsmethode nicht immer genau bestimmen.
Die folgende Grafik visualisiert das Gleichungssystem:
      I:  y = 2x + 2
     II: 5x - y = 0


Der exakte Schnittpunkt ist aus der Grafik nur schwer heraus zu lesen. 

Es ist daher erfordelich, Gleichungssysteme
auch rechnerisch lösen zu können!

Im Laufe des Kapitels werden wirst du nun 3 verschiedene
Lösungsverfahren kennen lernen!

Wir betrachten das folgende Beispiel:

    I: y = 4x + 2 
   II: y = 5x



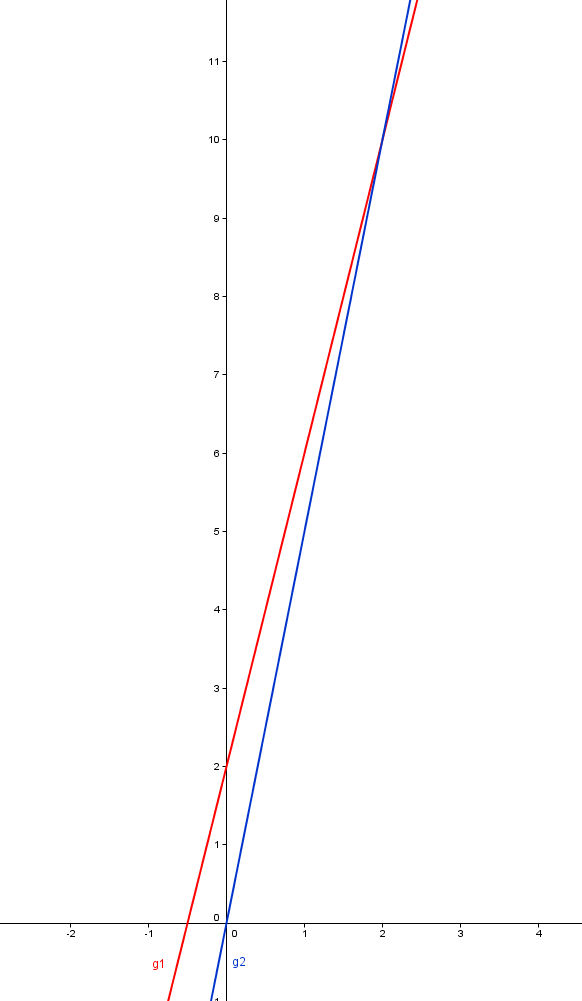Auch hier tritt das Problem auf, dass man den Schnittpunkt nicht exakt von
der Grafik ablesen kann!

Man kann sich nun aber folgendes überlegen:
Im Schnittpunkt der beiden Geraden haben beide Gleichungen denselben y-Wert.
Das bedeutet auch, dass die Werte der Terme 4x + 2 und 5x gleich sind!

Die folgenden Bilder zeigen, wie man die Lösung dieses Gleichungssystems auch mit Hilfe eines 
Waagenmodells veranschaulichen kann!


Da die Werte der Terme 4x + 2 und 5x also gleich sind, kann man 
die beiden Terme  gleichsetzen ! 
So entsteht eine Gleichung mit nur einer Variablen und zwar:
    4x + 2 = 5x

Formt man die Gleichung auf x um, so erhält man x = 2

Durch das Rückeinsetzen von x in die erste oder zweite Gleichung 
des Gleichungssystems, erhält man auch für y einen Zahlenwert:
     I: y = 4*2 + 2 = 10
oder
    II: y = 5*2 = 10

Die beiden Geraden schneiden sich also im Punkt S(2|10).
Die Lösungsmenge des Gleichungssystems lautet daher: L = {(2|10)}

Auch ein Gleichungssstem wie folgendes kann man mit dem 
Gleichsetzungsverfahren lösen:
    I:  y + 2x = 1
   II: 2y = 6x + 4

(1) 
Zuerst sollte das Gleichungssystem entweder nach x oder nach y aufgelöst werden:
Nachdem man das Gleichungssystem nach x aufgelöst hat, sieht es so aus:
    I: x = -y/2 + 1/2
   II: x = y/3 - 2/3
Nachdem man das Gleichungssystem nach y aufgelöst hat, sieht es so aus:
    I: y = -2x + 1
   II: y = 3x + 2

(2) 
Im Prinzip ist es egal, mit welchen der beiden umgeformten Gleichungssysteme man
weiterrechnet. Wir wählen hier die zweite Umformung, da diese keine Bruchzahlen 
beinhaltet und man sich somit beim Rechnen leichter tut.
Nun setzen wir die Terme auf der rechten Seite gleich:
   -2x + 1 = 3x + 2

(3)
Man hat somit wieder eine Gleichung mit nur einer Unbekannten und kann
diese Gleichung nach x auflösen:
   -2x + 1 = 3x + 2
       -5x = 1
         x = -10,2

(4)
Als nächstes kann man den Wert von y berechnen, indem man eintweder in die 
erste oder in die zweite Gleichung einsetzt. Das Einsetzen in die erste Gleichung liefert:
   y = -2*(-0,2)+1
   y = 1,4

(5)
Die Lösungsmenge des Gleichungssystems lautet also: L = {(-0,2|1,4)}

(6)
Um deine Lösung zu überprüfen, kannst du sie in die beiden Ausgangsgleichungen einsetzen:
    I: 1,4 + 2*(-0,2) = 1  -> wahr!
   II: 2*1,4 = 6*(-0,2) + 4

Wir betrachten folgendes Beispiel:

    I:  y - x = 2
   II: 2y + 5 = 5x


Möglichkeit 1:
(1)
Wir formen die erste Gleichung nach y um:
   y = x + 2

(2)
Als nächstes setzen wir anstelle von y den Term (x + 2) in die zweite Gleichung ein! 
Wir erhalten somit eine Gleichung mit nur einer Variablen.

Die folgenden Bilder zeigen, wie man diese Überlegung auch mit Hilfe eines 
Waagenmodells veranschaulichen kann!


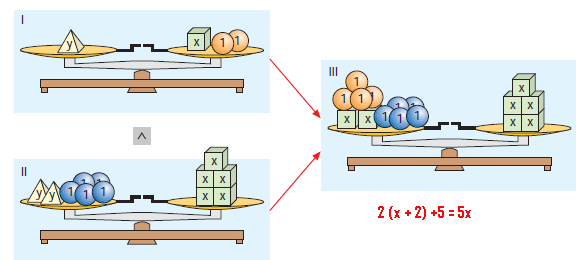(3)
Diese Gleichung können wir nun nach x lösen:
   2(x + 2) + 5 = 5x
     2x + 4 + 5 = 5x
              9 = 3x
              3 = x
(4)
Um einen Wert für y zu erhalten, müssen wir x einfach in eine der beiden Gleichungen einsetzen:
   y = x + 2 = 3 + 2 
   y = 5

Die Lösungsmenge des linearen Gleichungssystems ist somit: L = {(3|5)}


Möglichkeit 2:
(1)
Wir formen die erste Gleichung nach x um:
   x = y - 2

(2)
Danach setzen wir anstelle von x den Term (y - 2) in die zweite Gleichung ein:
   2y + 5 = 5(y - 2)

(3)
Diese Gleichung kann nach y aufgelöst werden:
   2y + 5 = 5(y - 2)
   2y + 5 = 5y - 10
       3y = 15
        y = 5
(4)
Um einen Wert für x zu erhlaten, müssen wir y einfach in eine der beiden Gleichungen einsetzen:
   x = y - 2 = 5 - 2
   x = 3

Wir erkennen: Auch hier ist die Lösungsmenge des linearen Gleichungssystems: L = {(3|5)}

Wir betrachten das folgende Beispiel:

     I: 2x + 3 = 2y + 5
    II: 2y + 1 = x + 2

Wir überlegen uns folgendes:
Wenn (2x + 3) gleich (2y + 5) ist und (2y + 1) gleich (x + 2) ist, 
dann ist auch(2x + 3)+(2y + 1) gleich (2y + 5)+(x + 2)!

Sehen wir uns dazu auch eine Waagenmodell an:



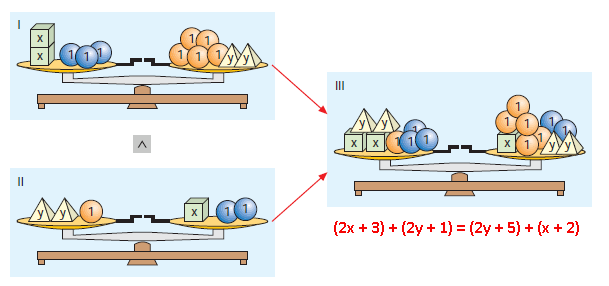Wenn man also jeweils die linken beiden Terme und die rechten beiden Terme eines
Gleichungssystems addiert, erhält man wieder eine richtige Gleichung!
Also:
    (2x + 3)+(2y + 1) = (2y + 5)+(x + 2)
          2x + 2y + 4 = x + 2y + 7 

Was uns bei dieser Gleichung sehr entgegenkommt ist, dass auf der linken UND auf der 
rechten Seite der Gleichung der Term 2y vorkommt! Zieht man von beiden Seiten der
Gleichung 2y ab, so erhält man:
    2x + 4 = x + 7        

Das ist nun eine Gleichung mit nur einer Variablen! Lösen wir sie nach x auf,
erhalten wir:
    x = 3

Um einen Wert für y zu erhalten, setzen wir x in eine der beiden Gleichungen ein:
Einsetzen in die zweite Gleichung liefert:
    2y + 1 = 3 + 2
        2y = 4
         y = 2

Die Lösungsmenge des linearen Gleichungssystems ist somit L = {(3|2)}.

Das Beispiel, das wir in 3.7 gelöst haben, war sehr praktisch! 
In beiden Gleichungssystemen kam der Ausdruck 2y vor, und zwar genau so, 
dass dieser Audruck wegfiel, als man die beiden Gleichungen miteinander addierte!

Aber was müssen wir tun, wenn wir ein Gleichungssystem, das nicht so "praktisch" ist,
mit dem Additionsverfahren lösen wollen?

Betrachten wir folgendes Beispiel:

     I: 2x + 4y = 10
    II: 3x + 5y = 14

Würden wir bei diesem Gleichungssystem die beiden linken und die beiden
rechten Seiten zusammenzählen, würde dabei folgende Gleichung herauskommen:
    (2x + 4y) + (3x + 5y) = 10 + 14
                  5x + 9y = 24  

Wir würden also eine Gleichung mit zwei Variablen erhalten!
Und wie wir bereits aus dem ersten Kapitel wissen, lässt sich so eine Gleichung
nicht eindeutig lösen.
Wir müssen uns daher etwas anderes überlegen:
Wenn man eine Gleichung mit einer Zahl multipliziert, ändert sich ja bekanntlich ihr Wert nicht.
Multiplizieren wir also die erste Gleichung mit 3 und die zweite Gleichung mit (-2):
     I: 2x + 4y = 10   |*3
    II: 3x + 5y = 14   |*(-2)
   --------------------
     I: 6x + 12y = 30
    II:-6x - 10y = -28

Addieren wir diese beiden veränderten Gleichungen miteinander, ergibt sich folgendes:
    (6x + 12y) + (-6x - 10y) = 30 + (-28)
                          2y = 2
                           y = 1

Dadurch, dass wir die Gleichungen jeweils mit 3 und (-2) multipliziert haben, haben wir erreicht,
dass die Koeffizient von x entgegengesetzt gleich sind! Aus diesem Grund fällt die Variable x 
auch weg, wenn man die beiden Gleichungen addiert!

Um das Gleichungssystem noch vollständig zu lösen, setzen wir y noch in eine
der beiden Gleichungen ein:
    2x + 4 = 10
         x = 3

Die Lösungsmenge des Gleichungssystems lautet somit: L = {(3|1)}



  

    

Folgerung:
Beim Additionsverfahren multipliziert man - wenn nötig - beide Gleichungen
eines Gleichungssystems mit geeigneten Zahlen, sodass die Koeffizienten
einer Variablen eingegengesetzt gleich werden!
Beim Addieren beider Gleichungen fällt eine Variable weg und man erhält
dadurch eine Gleichung mit einer Variablen!

  


Überlege dir, mit welchen Zahlen du die Gleichungen in diesem Beispiel multiplizieren 
müsstest, damit die Koeffizienten von y entgegengesetzt gleich sind! Addierst du 
dann diese beiden Gleichungen miteinander, erhaltest du eine Gleichung, die nur mehr
von x abhängt. Im Endeffekt muss dieselbe Lösungmenge herauskommen!

Wir haben in diesem Kapitel bis jetzt nur Gleichungssysteme betrachtet, deren
Lösungsmenge aus einer einzigen Lösung bestand. Aus dem Kapitel 2 wissen wir aber, 
dass es für Gleichungssysteme mit 2 Variablen noch zwei weitere Lösungsmöglichkeiten gibt!


Das Gleichungssystem ist unlösbar:

Wir lösen das folgende Gleichungssystem rechnerisch und grafisch und vergleichen:
     I: -2x + 3y = 6
    II: 2x - 3y = 3

Nachdem wir das Additionsverfahren angewendet haben, erhalten wir folgendes:
    (-2x + 3y) + (2x - 3) = 6 + 3
                        0 = 9   !falsche Aussage!

Auch beim Einsetzungsverfahren und beim Gleichsetzungsverfahren fallen die Variablen weg und man
erhält eine falsche Aussage! Das Gleichungssystem ist daher unlösbar: L = {}

Aus dem zweiten Kapitel wissen wir, dass ein Gleichungssystem genau dann unlösbar ist, 
wenn die beiden Geraden zueinander parallel sind! 
Wir überprüfen das zusätzlich, indem wir das Gleichungssystem auch nóch grafisch lösen:

Formen wir zuerst die Gleichungen um:
     I: y = 2x/3 + 2
    II: y = 2x/3 - 1

Die Parallelität der Geraden lässt sich hier anhand der Gleichung schon sehr gut 
erkennen: Die Steigungen sind jeweils gleich, aber der Schnittpunkt mit der 
y-Achse (oft d genannt) ist unterschiedlich.

Die Grafik bestätigt unsere Rechnung: Die Geraden sind parallel!



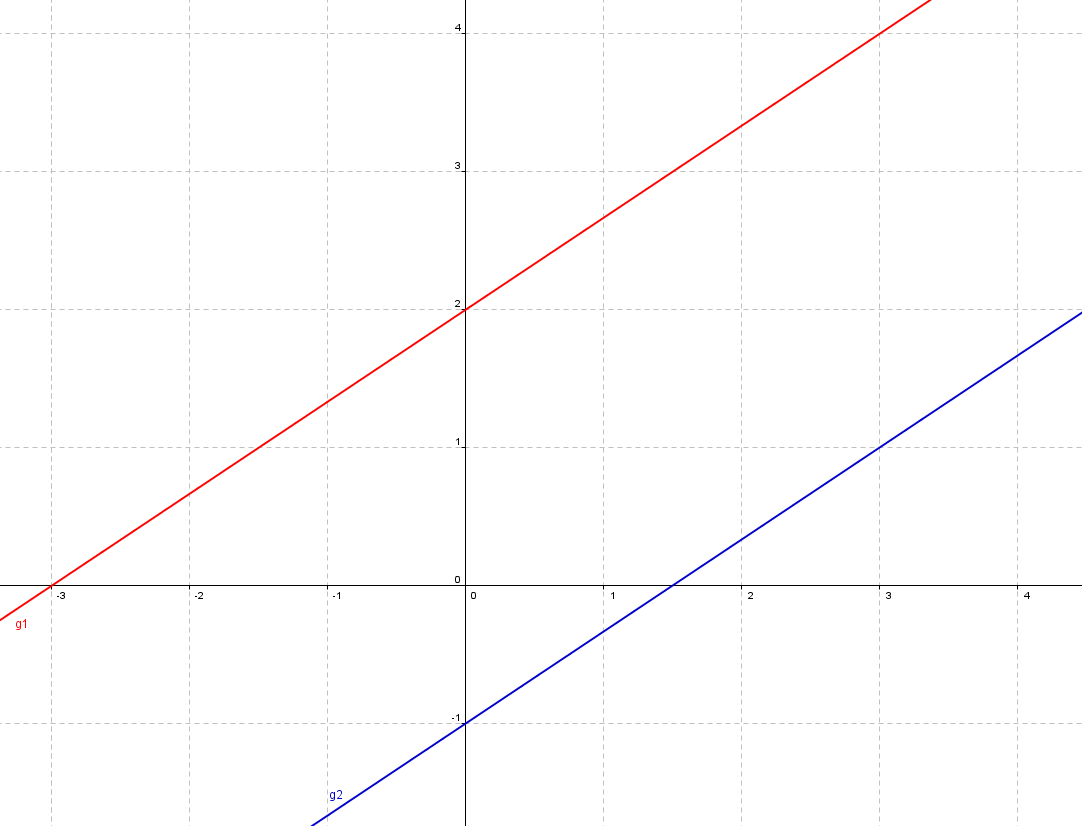Das Gleichungssystem hat unendlich viele Lösungen:

Um diesen Fall zu besprechen lösen wir folgendes Gleichungssystem rechnerisch und grafisch:
     I: 2x +  y = 5
    II: 4x + 2y = 10

Wir verwenden das Additionsverfahren und multiplizieren die erste Gleichung mit (-2):
     I: -4x - 2y = -10
    II:  4x + 4y =  10
   --------------------
               0 = 0   !wahre Aussage!

Zum selben Ergebnis kommen wir, wenn wir eines der beiden anderen Verfahren 
verwenden!

Beide Variablen x und y und die Konstante fallen weg, weil die zweite Gleichung
ein Vielfaches der ersten Gleichung ist. Es bleibt daher nur eine Gerade übrig,
oder anders ausgedrückt: die beiden Geraden sind identisch.

Alle Zahlenpaare, die die Gleichung 2x + y = 5 erfüllen, sind Lösungen
des Gleichungssystems. Es gibt daher unendlich viele Lösungen:
L = {(x|y) | y = -2x + 5}

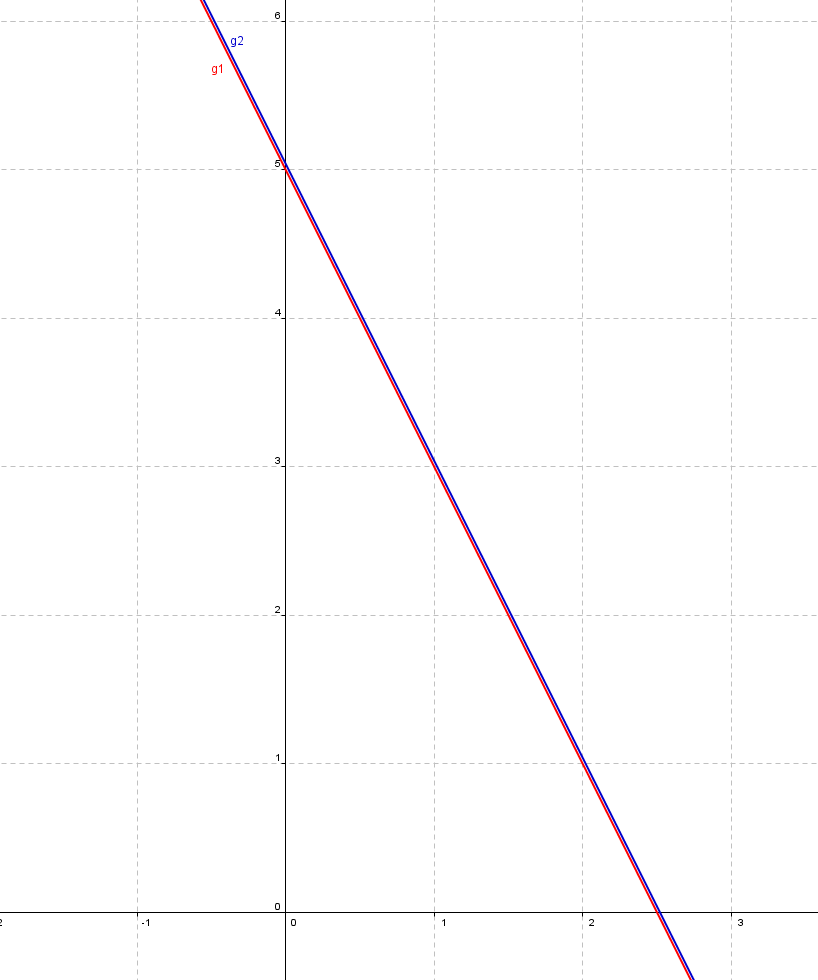
Wenn wir das Gleichungssystem wieder visualisieren, können wir uns nocheinmal 
davon überzeugen, dass die beiden Gleichungen (Geraden) identisch sind:
 

Überprüfe, ob du die unterschiedlichen Lösungsmöglichkeiten 
verstanden hast!

Löse die Gleichungssysteme und interpretiere die Lösungen!