|
4.1 Zahlenrätsel - Musterbeispiele und Denkanstöße
|

 

|
Beispiel 1:
Die Summer zweier Zahlen ist 20.
Das Doppelte der einen Zahl ist gleich dem 3-fachen der anderen Zahl.
Wie heißen die beiden Zahlen?
Wir bezeichnen die Zahlen mit x und y:
1. Beziehung = Gleichung I: x + y = 20
2. Beziehung = Gleichung II: 2x = 3y
Wir formen die erste Gleichung um und verwenden das Einsetzungsverfahren:
I: x = 20 - y
I in II einsetzen: 2*(20 - y) = 3y
Nach dem Lösen dieser Gleichung erhalten wir: y = 8
Wir setzen y in die erste Gleichung ein: x = 12
Probe: I: 12 + 8 = 20 -> wahr!
II: 2*12 = 3*8 -> wahr!
Anwort: Die Zahlen x = 12 und y = 8 sind die Lösungen des Gleichungssstems.
Beispiel 2:
Zwei Zahlen verhalten sich wie 2:3.
Subtrahiert man von jeder Zahl 6, so verhalten sich die neuen Zahlen wie 1:2.
Wie heißen die beiden Zahlen?
Wir bezeichnen die Zahlen mit x und y:
1. Bedingung: I: x:y = 2:3 -> 3x = 2y
2. Bedingung: II: (x - 6):(y - 6) = 1:2 -> 2*(x - 6) = y - 6
Nun muss man das Gleichungssystem nur mehr lösen!
Lernstoff
|
|
4.3 Gleichungen aus der Geometrie - Musterbeispiele und Denkanstöße
|

 

|
Beispiel 1:
In einem gleichschenkeligen Dreieck ist der Basiswinkel a
doppelt so groß wie der Scheitelwinkel g.
Berechne die Größe der Winkel im Dreieck!
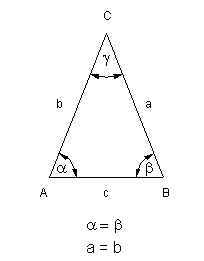 1. Bedingung:
Die Winkelsumme in einem Dreieck ist immer 180°!
=> I: 2a + g = 180
2. Bedingung:
=> II: a = 2g
Die Variablen in diesem Gleichungssystem heißen nun a und g.
Das Gleichungssystem kann auf gewohnte Art und Weise gelöst werden!
Beispiel 2:
Verlängert man die längere Seite eines Rechtecks um 4cm und die kürzere Seite um 2cm,
so wächst der Flächeninhalt um 64cm².
Verlängert man aber die längere Seite des Rechtecks um 8cm und die kürzere um 3cm,
so wächst der Flächeninhalt um 124cm².
Berechne die Seitenlängen des Rechtecks!
1. Bedingung:
Die Winkelsumme in einem Dreieck ist immer 180°!
=> I: 2a + g = 180
2. Bedingung:
=> II: a = 2g
Die Variablen in diesem Gleichungssystem heißen nun a und g.
Das Gleichungssystem kann auf gewohnte Art und Weise gelöst werden!
Beispiel 2:
Verlängert man die längere Seite eines Rechtecks um 4cm und die kürzere Seite um 2cm,
so wächst der Flächeninhalt um 64cm².
Verlängert man aber die längere Seite des Rechtecks um 8cm und die kürzere um 3cm,
so wächst der Flächeninhalt um 124cm².
Berechne die Seitenlängen des Rechtecks!
| |
Basisrechteck |
Rechteck 1 |
Rechteck 2 |
| Länge: |
x |
x + 4 |
x + 8 |
| Breite: |
y |
y + 2 |
y + 3 |
| Flächeninhalt: |
A0=x*y |
A1=(x+4)*(y+2) |
A2=(x+8)*(y+3) |
Aus dem Angabentext lesen wir, dass A1 um 64cm² größer ist als A0.
Gibt man also zu A0 64cm² dazu, sind beide Rechtecke gleich groß:
=> I: A0 + 64 = A1
I: x*y + 64 = (x+4)*(y+2)
Außerdem wissen wir aus der Angabe, dass A2 um 124cm² größer als A0 ist:
=> II: A0 + 124 = A2
II: x*y + 124 = (x+8)*(y+3)
Und so erhalten wir ein Gleichungssystem mit 2 Variablen, dass wir wieder
wie gewohnt lösen können!
Lernstoff
|
|
4.5 Gleichungen aus dem Alltag - Musterbeispiele und Denkanstöße
|

 

|
Beispiel 1:
Max möchte wissen, wie viel Geld seine Schwester Claudia in ihrem Sparschwein hat!
Claudia sagt: ,,Wenn ich dir 1€ gebe, dann haben wir beide gleich viel. Wenn du
mir 1€ gibst, dann habe ich doppelt so viel wie du!''
Wie viel Geld hat Claudia und wie viel Geld hat Max?
| jetzt |
I: Claudia gibt Max 1€ |
II: Max gibt Claudia 1€ |
| Claudia: c |
c - 1 |
c + 1 |
| Max: m |
m + 1 |
m - 1 |
|
beide haben gleich viel:
c - 1 = m + 1
|
Claudia hat doppelt so viel wie Max:
c + 1 = 2*(m - 1)
|
Das Gleichungssystem lautet also:
I: c - 1 = m + 1
II: c + 1 = 2*(m - 1)
Beispiel 2:
Auf einem Bauernhof gibt es Hühner und Kaninchen mit zusammen 25 Köpfen und 68 Beinen.
Wie viele Hühner und wie viele Kaninchen gibt es?
|
Köpfe: |
Beine: |
| Anzahl der Hühner: h |
h |
2h |
| Anzahl der Kaninchen: k |
k |
4k |
| zusammen: |
h + k |
2h + 4k |
Das Gleichungssystem lautet also:
I: h + k = 25
II: 2h + 4k = 68
Lernstoff
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



