|
1.1 Einleitung
|

 

|
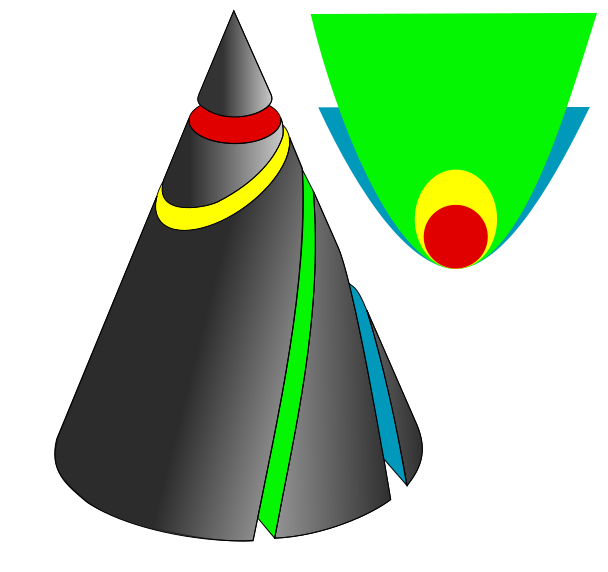
Kegelschnitte entstehen, wie der Name schon sagt, aus einem Schnitt mit einem Kegel und einer Ebene.
Es gibt 3 verschiedene Arten von Kegelschnitte: Parabel, Ellipse und Hyperbel.
Im Alltag können wir auch sehr oft Kegelschnitte beobachten. Zum Beispiel die Wurfbahn eines nach schräg oben geworfenen Balls beschreibt eine Parabel. Oder die Oberfläche von Saft, in einem runden Glas, das schief gehalten wird, beschreibt eine Ellipse und bei einem Stift, der gespitzt wird, ist die entstehende Kurve eine Hyperbel.


|
|
1.2 Geschichte der Kegelschnitte
|

 

|
Als Entdecker der Kegelschnitte gilt Menaichmos (360 v. Chr.). Er löste das Problem der Würfelverdopplung und stieß dabei auf die Kurven der Kegelschnitte.
Bereits Aristaios (um 300 v. Chr.), sowie auch Euklid (ca 300 v. Chr.) verfassten ein Buch zum Thema Kegelschnitte. Leider sind diese beiden Texte bis heute nicht erhalten geblieben.
Vor allem Archimedes (287 - 212 v. Chr.) hat sich intensiv mit den Kegelschnitten auseinandergesetzt. Unter anderem bestimmte er die Fläche des Parabelsegments und berechnete die Fläche der Ellipse. Auch den Inhalt der Kugel, der Rotationsflächen 2. Grades und anderer Körper konnte er bestimmen.
Ursprünglich betrachtete man diese Fälle, in denen die Schnittebene auf eine Mantellinie des Kegels normal steht. Dementsprechend sprach man vom "Schnitt am rechtwinkeligen, spitzwinkeligen oder stumpfwinkeligen Kegel".
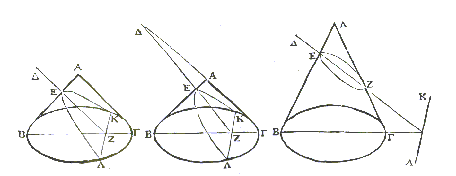
Apollonios von Perga (260 - 180 v. Chr.) lieferte die reifste Darstellung der Kegelschnitte und verfasste das Werk "Konika", bestehend aus 8 Büchern, von denen noch 7 erhalten sind. In diesem Werk führte er zum ersten Mal die Begriffe Parabel, Ellipse und Hyperbel ein. Er zeigte in diesem Werk, dass man die 3 Arten der Kegelschnitte auch durch verschiedene Schnitte an einem Kegel erhalten kann. Auch beschäftigte er sich unter anderem mit Tangenten, Asymptoten, Pol und Polare.
Auch später untersuchte man noch immer die Eigenschaften der Kegelschnitte. Descartes (1596 - 1650) schuf mit der Analytischen Geometrie die Voraussetzung zur Untersuchung der Eigenschaften der Kegelschnitte anhand ihrer Gleichungen. Außerdem entdeckte er eine Methode zur Winkeldreiteilung mit Hilfe einer festen Parabel.
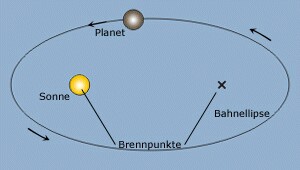
Johannes Kepler (1571 - 1630) beschäftigte sich mit den Kegelschnitten im Zusammenbhang mit den optischen Linsen. Danach entdeckte er sein erstes Bewegungsgesetz:
Die Planeten bewegen sich auf Ellipsen, in deren einem Brennpunkt die Sonne steht.
Der nach Blaise Pascal (1623 - 1662) bennante Satz über Sechsecke in einem Kegelschnitt wurde wichtig für die Entwicklung der projektiven Geometrie.
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



