|
3.1 Die Parabel
|

  
|
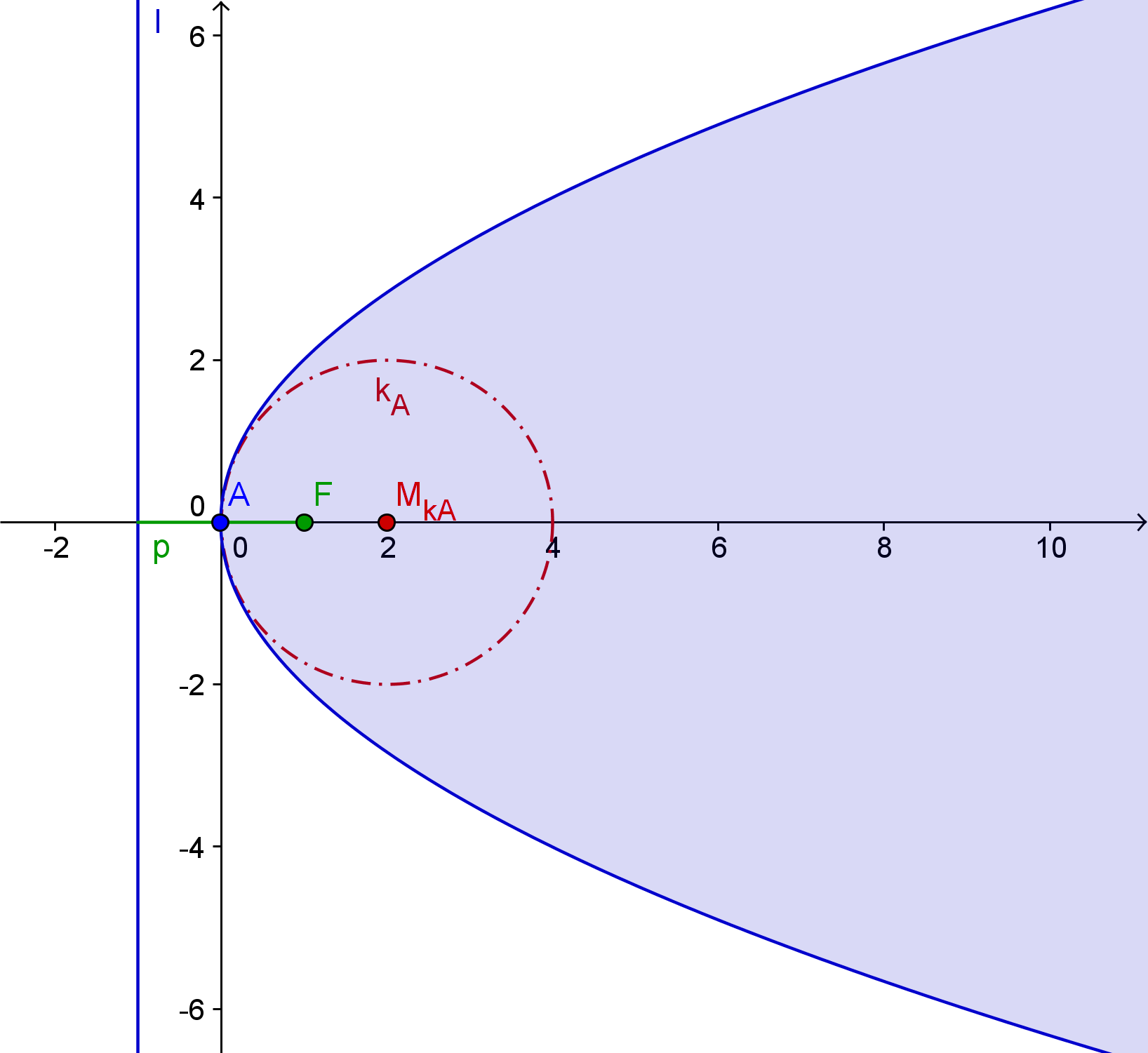
A . . . Scheitel
l . . . Leitgerade
F . . . Brennpunkt
MkA . . . Mittelpunkt des Scheitelkrümmungskreises
p . . . Abstand Fl
kA . . . Scheitelkrümmungskreis mit Radius p
Konstruktion der Parabel:
1.) Vom Scheitel A aus wird der Parameter p auf der y-Achse aufgetragen. Dadurch erhält man den Mittelpunkt des Scheitelkrümmungskreises MkA, der den Radius p hat.
2.) Nun kannst du die Parabel schon einzeichnen ☺
Unter diesem Link kannst du dir die Konstruktion noch mal Schritt für Schritt ansehen.
–––––––––––––––––––––––––––––
Aufgabe:
Zeichne mit Hilfe der Konstruktion in GeoGebra und der Konstruktionsbeschreibung eine Parabel in dein Schulübungsheft!
|
|
3.2 Die Ellipse
|

  
|
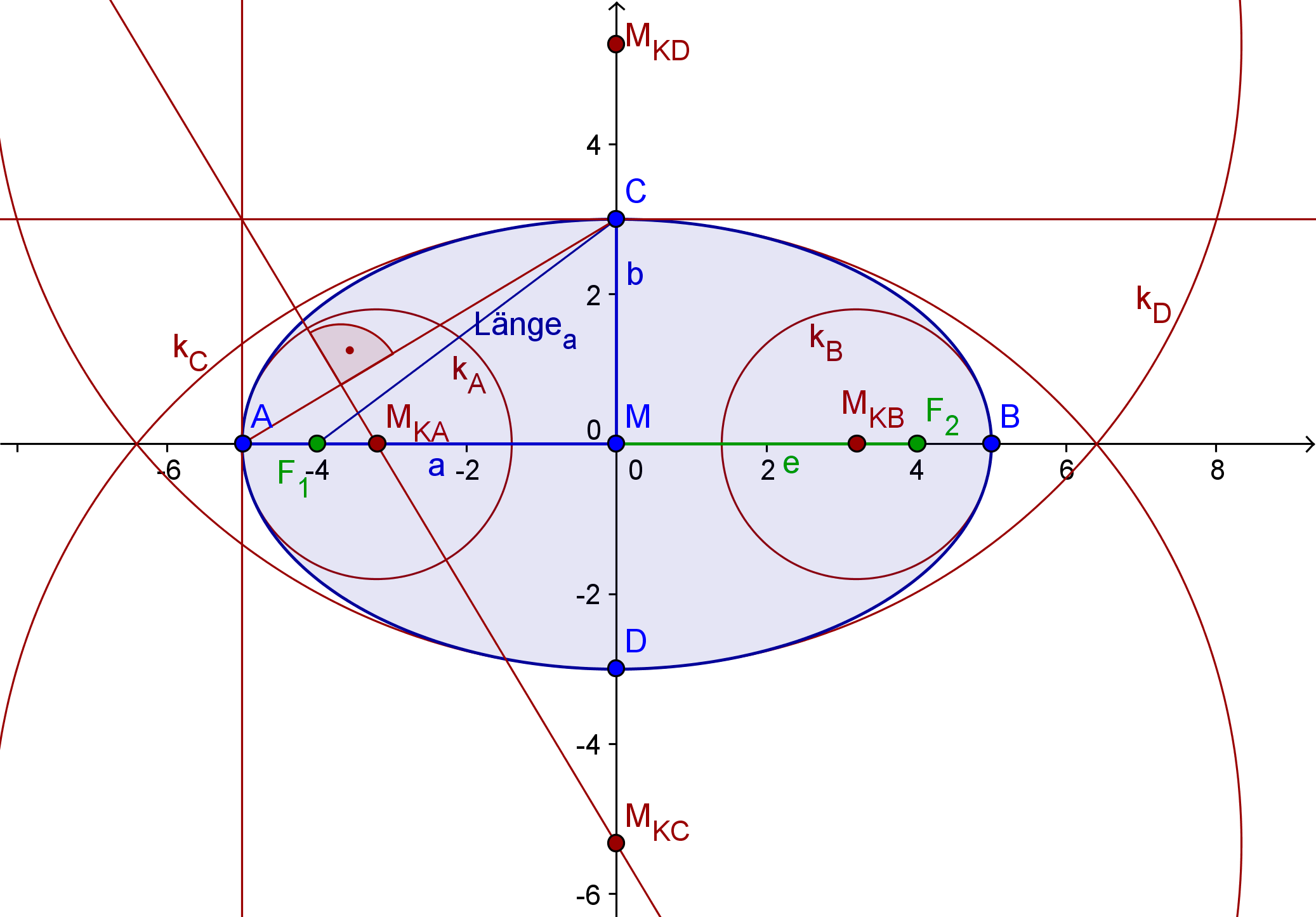
A, B . . . Hauptscheitel
C, D . . . Nebenscheitel
M . . . Mittelpunkt
a . . . | MA | = | MB | = | CF1 |
b . . . | MC | = | MD |
e . . . Brennweite = | MF1 | = | MF2 |
F1, F2 . . . Brennpunkte
MKA . . . Mittelpunkt vom Scheitelrümmungskreis in A
MKC . . . Mittelpunkt vom Scheitelkrümmungskreis in C
MKB . . . Mittelpunkt vom Scheitelkrümmungskreis in B
MKD . . . Mittelpunkt vom Scheitelkrümmungskreis in D
kA . . . Scheitelkrümmungkreis in A
kB . . . Scheitelkrümmungkreis in B
kC . . . Scheitelkrümmungkreis in C
kD . . . Scheitelkrümmungkreis in D
Konstruktion der Ellipse:
1.) Die Länge a wird von C aus auf der y-Achse aufgetragen. So erhälst du die Brennpunkte F1 und F2.
2.) Eine parallele Gerade zur y-Achse durch A und eine parallele Gerade zur x-Achse durch C ergeben einen Punkt.
3.) Man legt eine Normale zu AC durch diesen Punkt durch und schneidet sie mit der x-Achse und der y-Achse. Diese Punkte ergeben die Mittelpunkte der Scheitelkrümmungskreise MKA und MKC.
4.) Diese beiden Mittelpunkte werden am Mittelpunkt gespiegelt und man bekommt die Mittelpunkte der Scheitelkrümmungskreise MKB und MKD
5.) Die Scheitelkrümmungskreise können eingezeichnet werden.
6.) Jetzt hast du alle Konstruktionen, um die Ellipse konstruieren zu können ☺
Unter dem Link kannst du dir die Konstruktion wieder Schritt für Schritt ansehen.
–––––––––––––––––––––––––––––
Aufgabe:
Zeichne mit Hilfe der Konstruktion in GeoGebra und der Konstruktionsbeschreibung eine Ellipse in dein Schulübungsheft!
|
|
3.3 Die Hyperbel
|

  
|
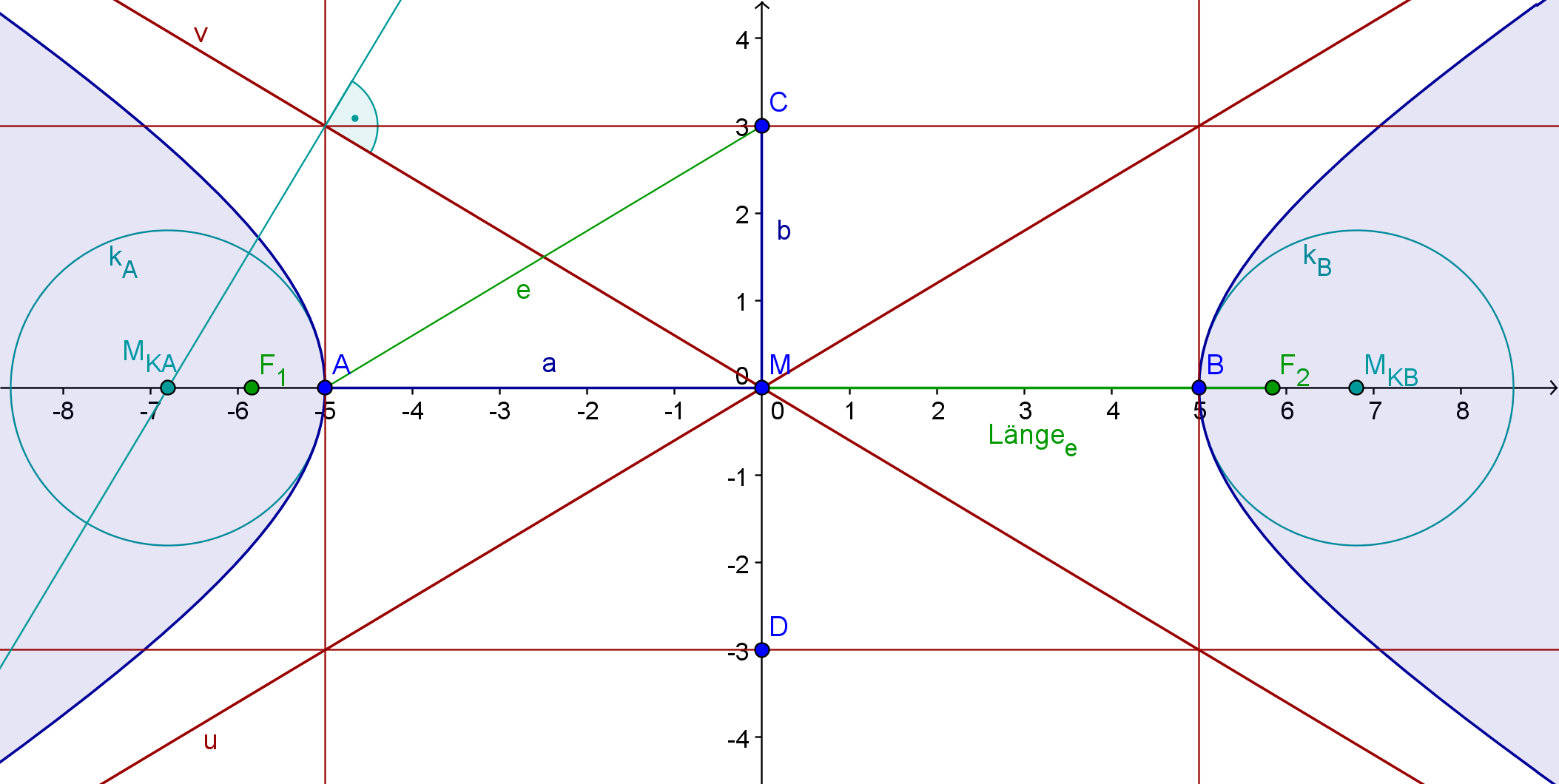
A, B . . . Hauptscheitel
C, D . . . Nebenscheitel
M . . . Mittelpunkt
a . . . | MA | = | MB |
b . . . | MC | = | MD |
e . . . Brennweite = | AC |
F1, F2 . . . Brennpunkte
u, v . . . Asymptoten
MKA . . . Mittelpunkt des Scheitelkrümmungskreises in A
MKB . . . Mittelpunkt des Scheitelkrümmungskreises in B
kA . . . Scheitelkrümmungskreis in A
kB . . . Scheitelkrümmungskreis in B
Konstruktion der Hyperbel:
1.) Die Länge AC = e wird von M aus auf der y-Achse aufgetragen. So erhälst du die Brennpunkte F1 und F2.
2.) Parallele Geraden zur y-Achse durch A und B, und parallele Geraden zur x-Achse durch C und D ergeben ein Rechteck.
3.) Durch die Eckpunkte des Rechtecks werden 2 Geraden gelegt, die die Asymptoten u und v der Hyperbel ergeben.
4.) Eine Normale auf eine Asymptote durch einen Eckpunkt (durch den die Asymptote geht) wird mit der x-Achse geschnitten. So erhält man den Mittelpunkt des Scheitelkrümmungskreise MKA.
5.) Der Mittelpunkt des Scheitelkrümmungskreises MKA wird an M gespiegelt. So bekommt man den Mittelpunkt des Scheitelkrümmungskreises MKB.
6.) Die Scheitelkrümmungskreise können eingezeichnet werden.
7.) Jetzt kannst du die Hyperbel konstruieren ☺
Unter dem Link kannst du dir die Konstruktion wieder Schritt für Schritt ansehen.
–––––––––––––––––––––––––––––
Aufgabe:
Zeichne mit Hilfe der Konstruktion in GeoGebra und der Konstruktionsbeschreibung eine Hyperbel in dein Schulübungsheft!
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



