|
2.1 Eigenschaften der Kegelschnitte
|

 

|
Die Parabel:
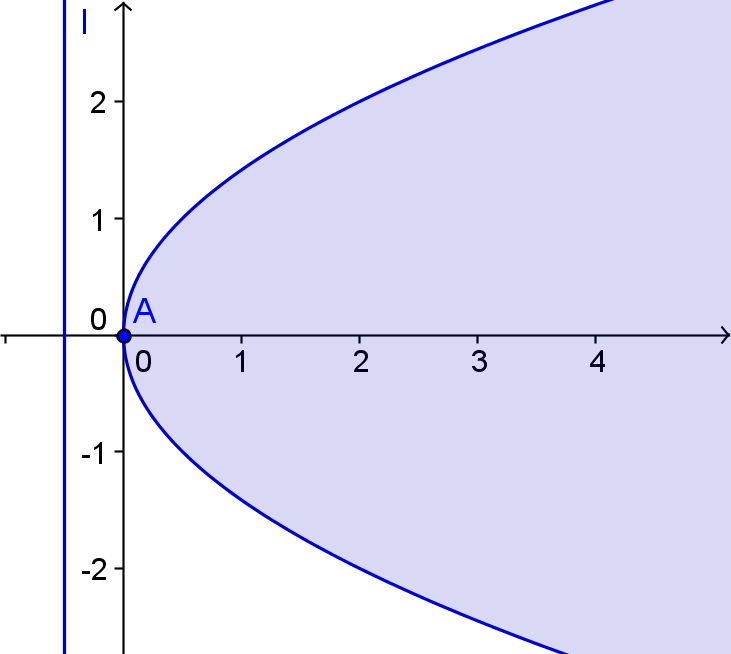
Die Parbel besitzt einen Scheitel A, oft auch S genannt, und eine Achse. Außerdem hat sie eine feste Gerade l, die Leitgerade genannt wird.
Die Ellipse:
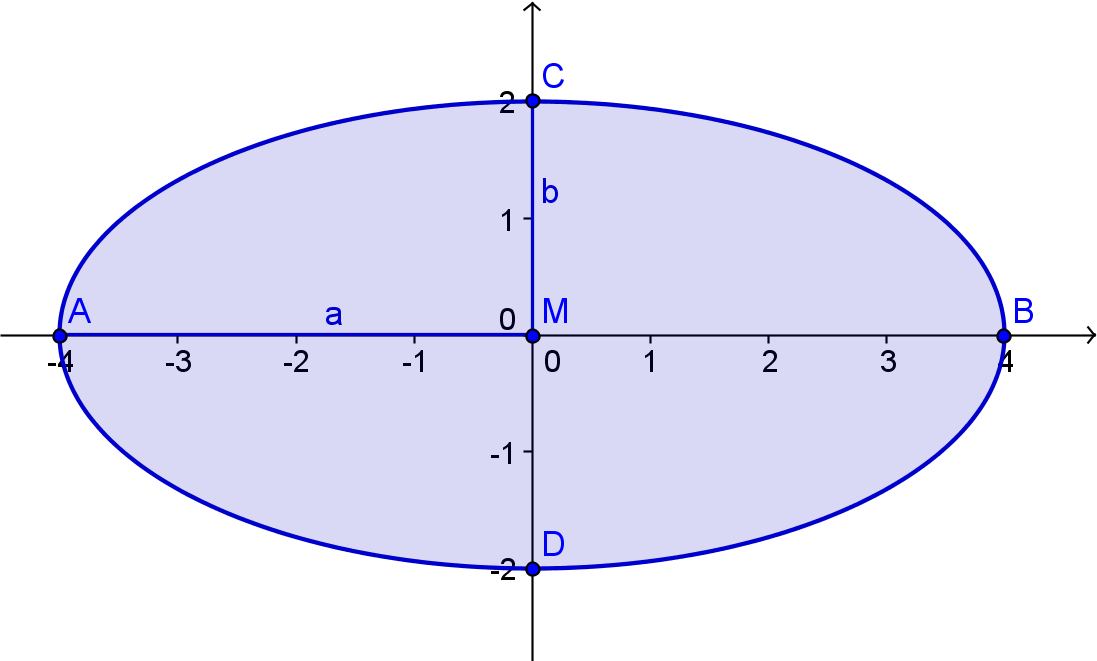
Die Ellipse hat vier Scheitel - genannt Hauptscheitel A und B, bzw. Nebenscheitel C und D.
Außerdem besitzt sie zwei Achsen: die Hauptachse, auf der die Hauptscheitel A und B liegen und die Nebenachse, auf der die Nebenscheitel C und D liegen.
Die Längen a und b werden auf den Achsen vom Mittelpunkt aus aufgetragen - a auf der Hauptachse und b auf der Nebenachse.
Ein Spezialfall der Ellipse ist der Kreis. Er entsteht, wenn a und b gleich lang sind.
Die Hyperbel:
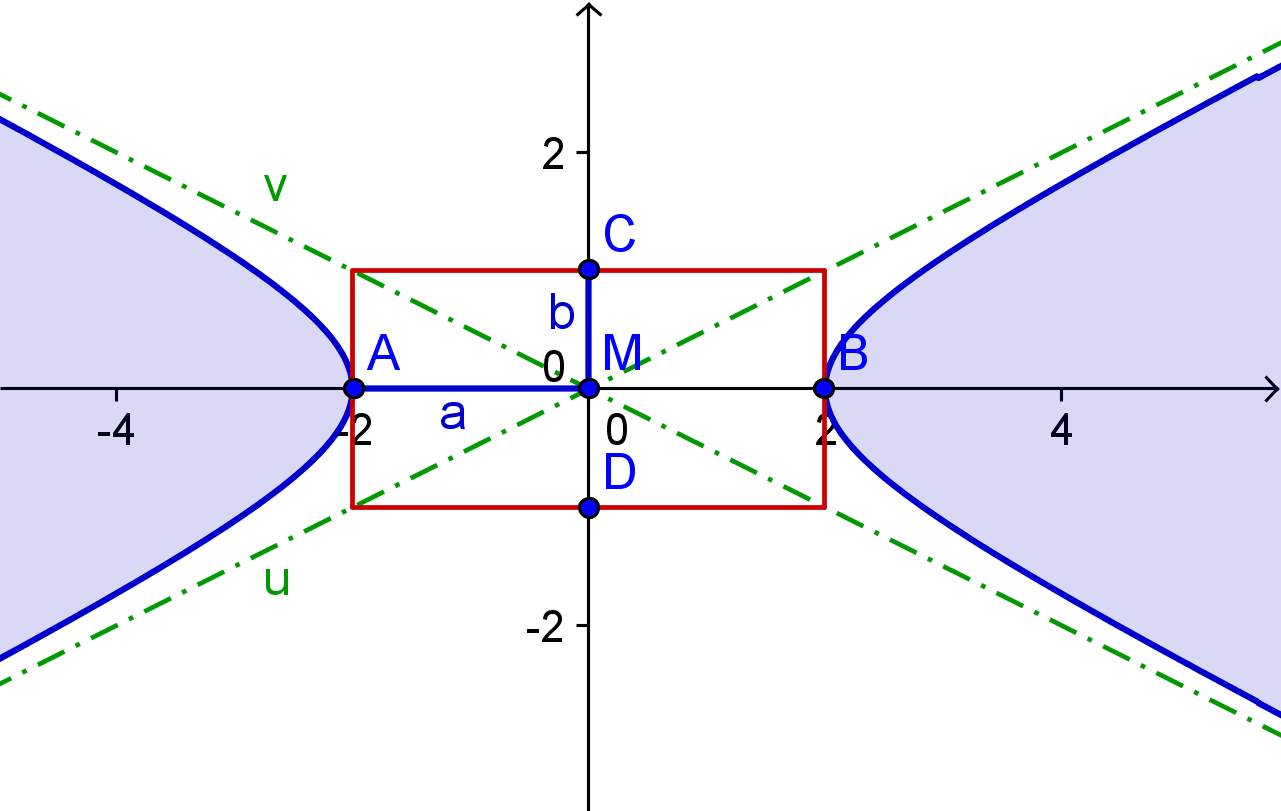
Auch die Hyperbel besitzt zwei Achsen - die Hauptachse und die Nebenachse, auf der sich die Hauptscheitel A, B und die Nebenscheitel C, D befinden.
Die Längen a bzw. b werden auf der Hauptachse bzw. der Nebenachse, jeweils vom Mittelpunkt M aus, aufgetragen.
Ein Rechteck, das durch A, B, C und D geht, kann nun eingezeichnet werden.
2 Asymptoten u und v gehen durch die Eckpunkte dieses Rechtecks. Das sind 2 Geraden, an denen sich die Hyperbel annähert, sie aber nie berührt.
Wenn a und b die gleich lang sind, dann stehen die Asymptoten im rechten Winkel zueinander.
Lernstoff
|
|
2.2 Die Parabel
|

  
|
Wenn α = β (die Schnittebene ist zu genau einer Mantellinie des Kegels parallel)
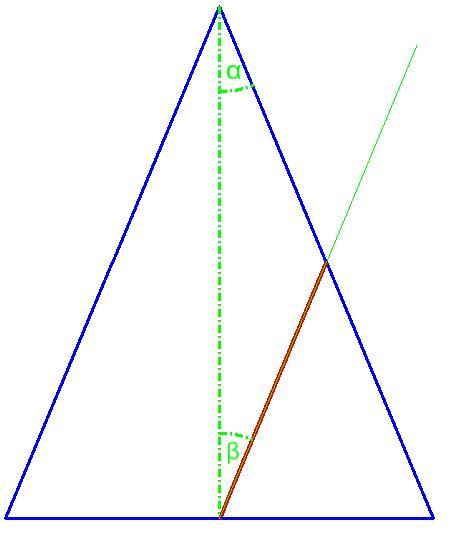

Definition
Die Parabel ist die Menge aller Punkte X, die zum Brennpunkt F den selben Abstand wie zur Leitgeraden l haben.
par = {X | XF = Xl}
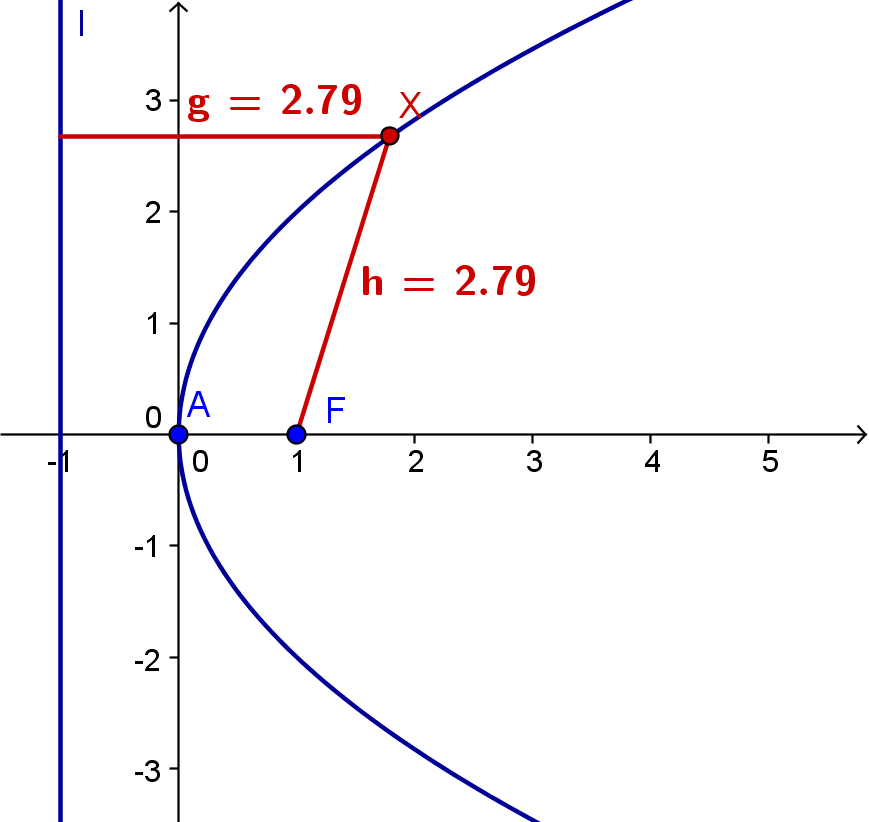
A . . . Scheitel
F . . . Brennpunkt
l . . . Leitgerade
Allgemeine Parabelgleichung
f(x) = ax² + bx + c für alle a, b, c aus den reellen Zahlen und a ≠ 0
Hauptlagen der Parabel
Es gibt 4 verschiedene Hauptlagen der Parabel.
1. Hauptlage: Der Scheitel A liegt im Koordinatenursprung und die Achse der Parabel ist die positive x-Achse.
Die Gleichung der Normparabel lautet: x = y²
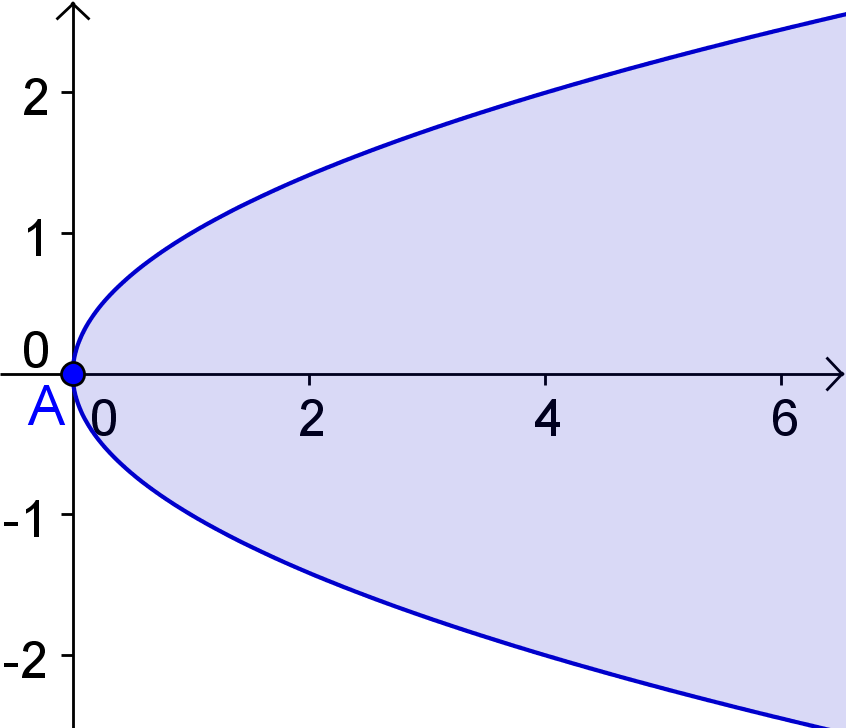
2. Hauptlage: Der Scheitel A liegt im Koordinatenursprung und die Achse der Parabel ist die positive y-Achse.
Die Gleichung der Normparabel lautet: y = x²
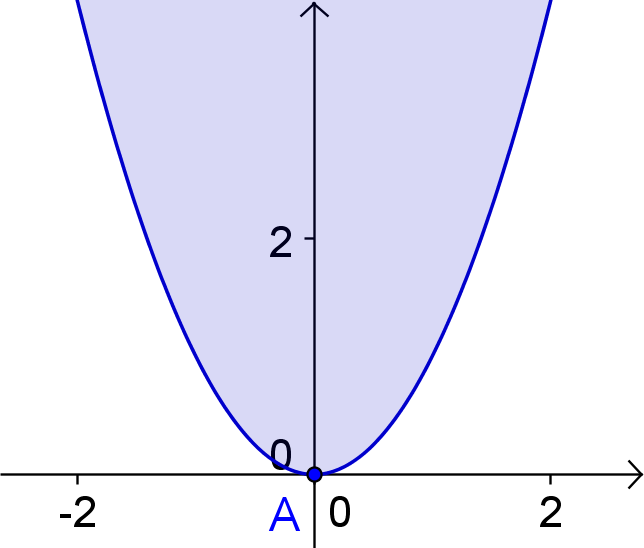
3. Hauptlage: Der Scheitel A liegt im Koordinatenursprung und die Achse der Parabel ist die negative x-Achse.
Die Gleichung der Normparabel lautet: x = -y²

4. Hauptlage: Der Scheitel A liegt im Koordinatenursprung und die Achse der Parabel ist die negative y-Achse.
Die Gleichung der Normparabel lautet: y = -x²
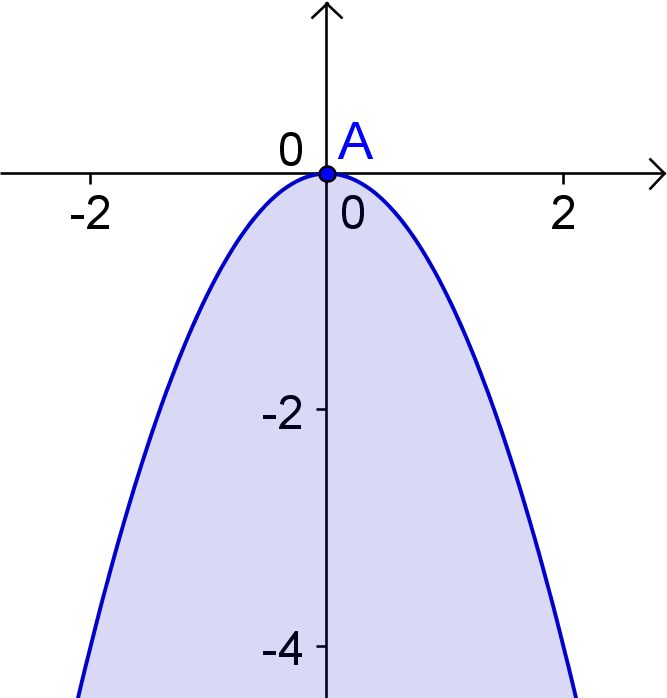
–––––––––––––––––––––––––––––
Aufgabe:
Schreibe die Formeln der Parabel in dein Schulübungsheft.
Versuche Skizzen der Parabel der 4 Hauptlagen in dein Heft zu zeichnen und schreibe die Formlen dazu.
Der folgende Link öffnet eine GeoGebra-Datei in der eine Parabel mit Schieberegler ist.
Bewege sie und schreibe dir die Veränderungen in dein Heft. Versuche mit der Konstruktion zu begründen, warum a nicht 0 sein darf!
Was passiert, wenn 1.) a = 0, b = 0 und c ≠ 0
2.) a = 0, b ≠ 0 und c = 0!
Parabel mit Schieberegler
|
|
2.3 Der Kreis
|

  
|
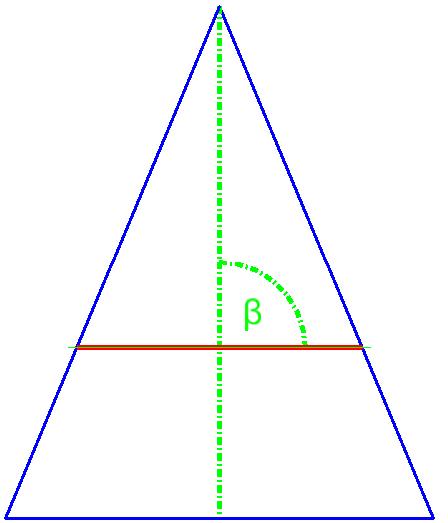
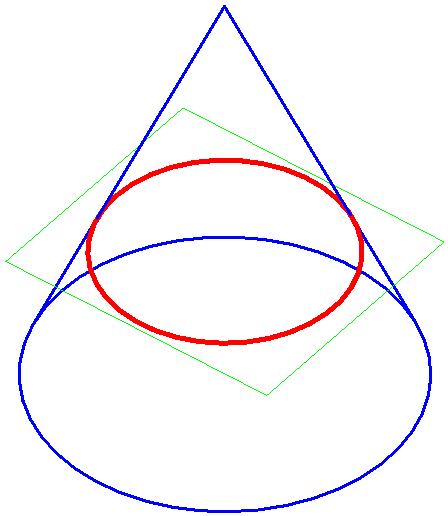
Wenn β = 90° (die Schnittebene steht im rechten Winkel zur Mittelachse des Kegels)
Definition
Der Kreis ist die Menge aller Punkte X, die von einem festen Punkt - den Mittelpunkt - den selben Abstand r haben.
k = {X | MX = r}
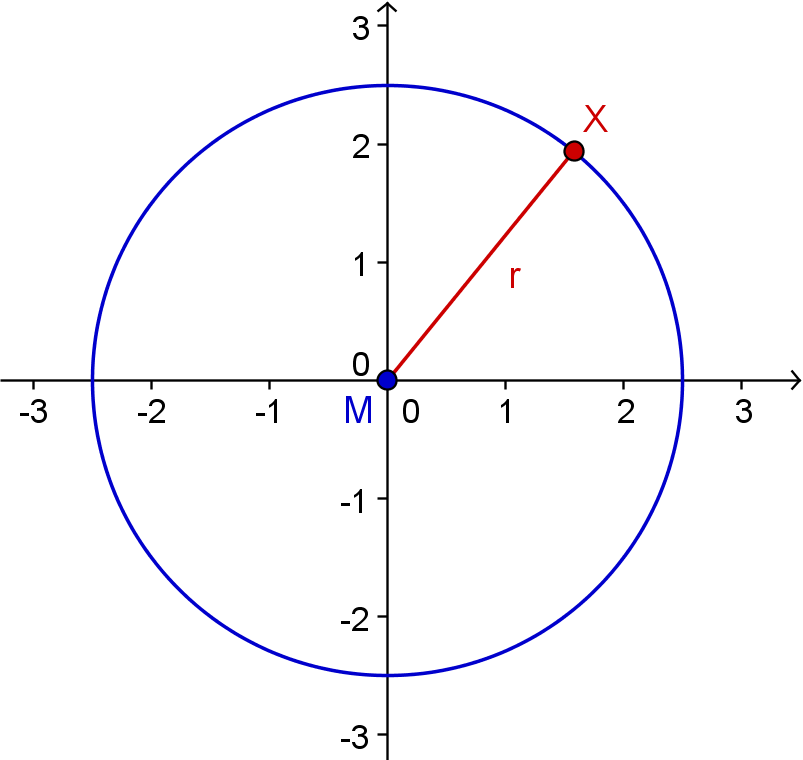
M . . . Mittelpunkt
r . . . Radius
Formeln des Kreises
Wenn der Mittelpunkt des Kreises im Koordinatenursprung liegt, dann lautet die Formel: x² + y² = r².
Ansonsten lautet die allgemeine Formel für den Kreis: (x - xm)² + (y - ym)² = r².
–––––––––––––––––––––––––––––
Aufgabe:
Schreibe die Formeln des Kreises in dein Schulübungsheft.
Zeichne mit Hilfe deines Zirkels einen Kreis in dein Heft und beschrifte ihn.
|
|
2.4 Die Ellipse
|

  
|
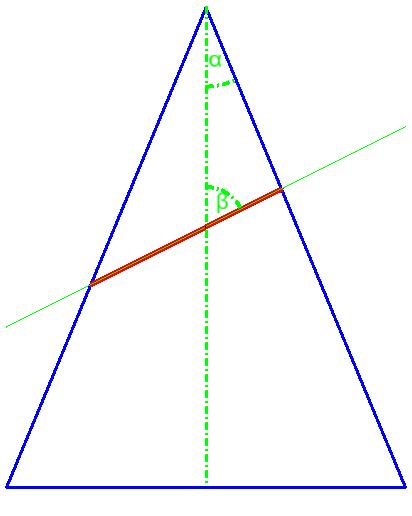
Wenn α < β (die Schnittebene ist zu keiner Mantellinie des Kegels parallel)
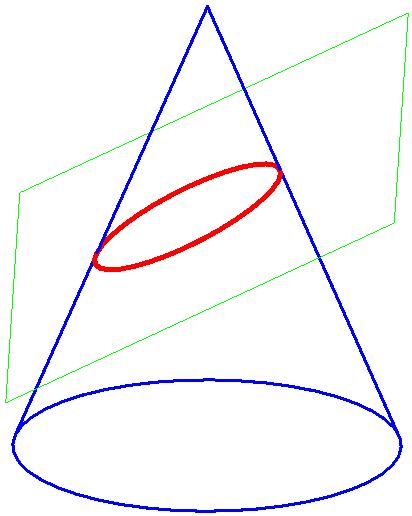
Definition
Die Ellipse ist die Menge aller Punkte X, für die die Summe der Abstände zu zwei festen Punkten - den Brennpunkten F1 und F2 - konstant ist.
ell = {X | F1X + F2X = 2a}
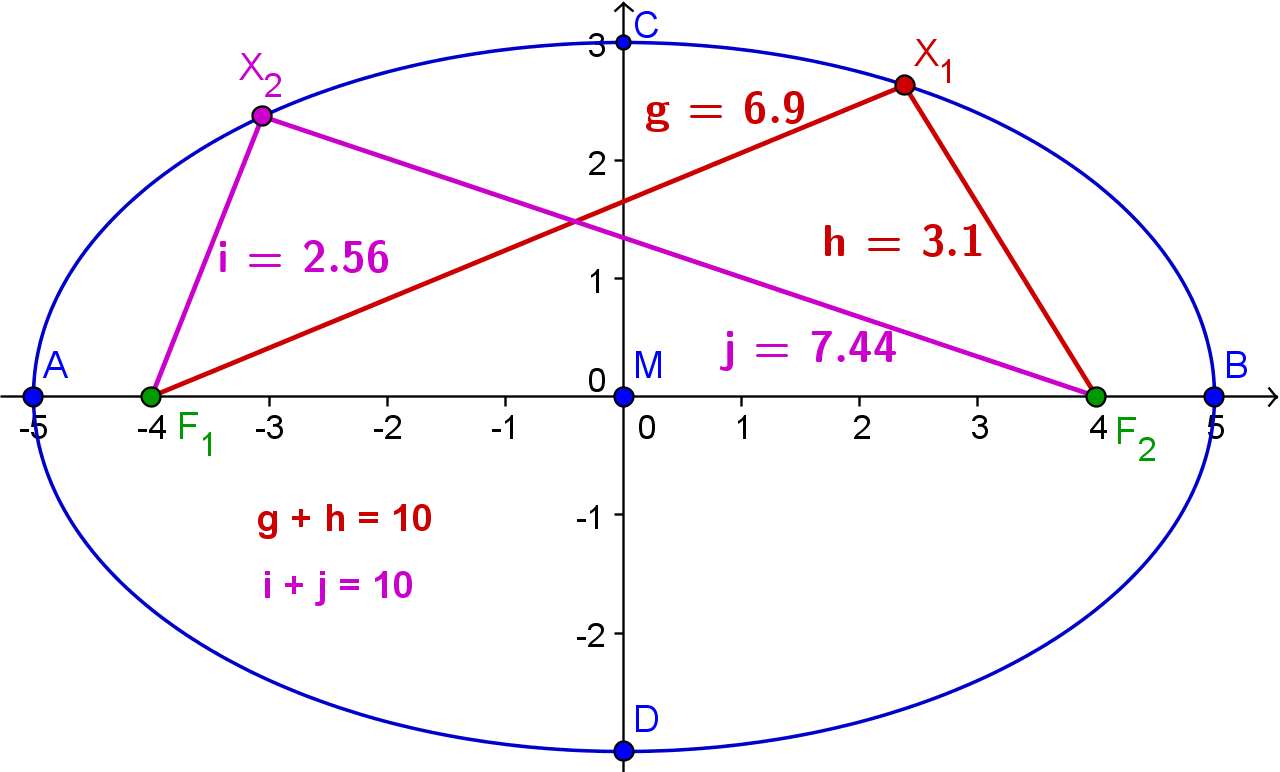
A, B . . . Hauptscheitel
C, D . . . Nebenscheitel
M . . . Mittelpunkt
F1, F2 . . . Brennpunkte
Hauptlagen der Ellipse
Es gibt 2 verschiedene Hauptlagen der Ellipse.
1.Hauptlage: Die Hauptachse liegt auf der x-Achse.
Die Gleichung der Ellipse lautet: x²/a² + y²/b² = 1.
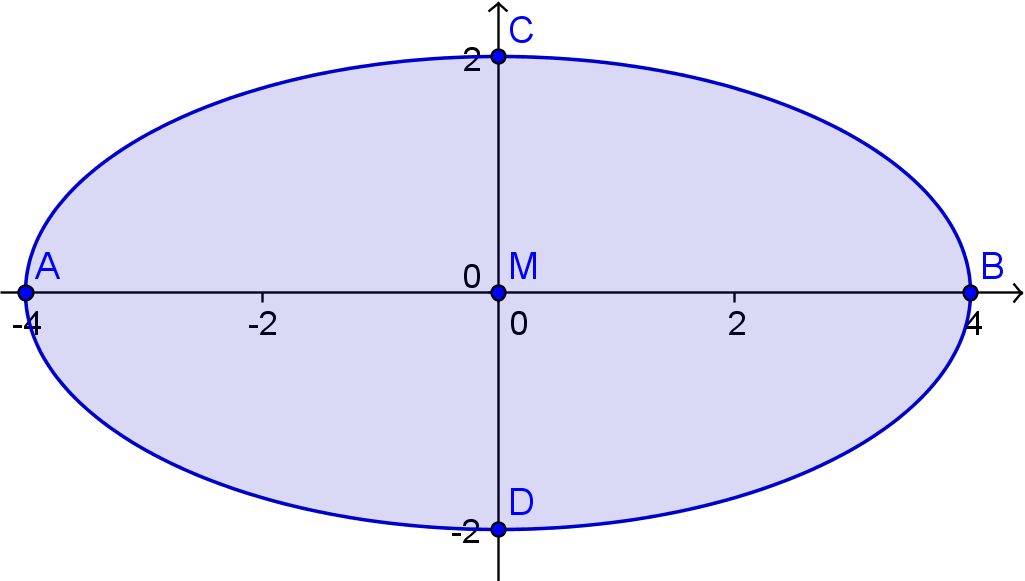
2.Hauptlage: Die Hauptachse liegt auf der y-Achse.
Die Gleichung der Ellipse lautet: x²/b² + y²/a² = 1.
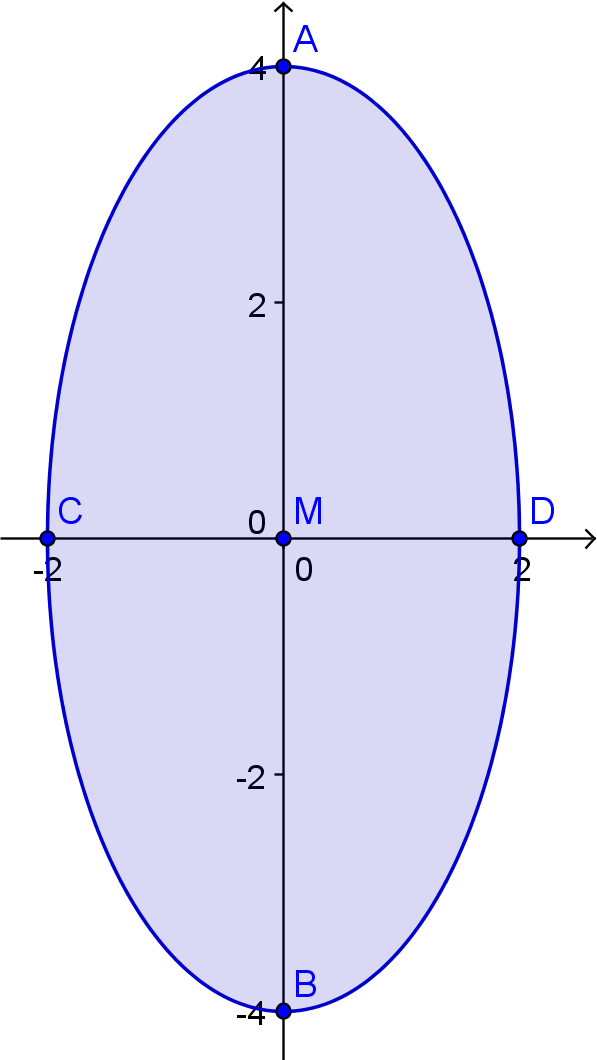
–––––––––––––––––––––––––––––
Aufgabe:
Schreibe die Formel der Ellipse in dein Schulübungsheft.
Versuche Skizzen der Ellipse der 2 Hauptlagen in dein Heft zu zeichnen und schreibe die Formlen dazu.
Der folgende Link öffnet eine GeoGebra-Datei in der eine Ellipse mit Schieberegler ist.
Bewege sie und schreibe dir die Veränderungen in dein Heft.
Was passiert mit der Ellipse, wenn 1.) a = 0 oder b = 0?
2.) a = b ist?
Ellipse mit Schieberegler
|
|
2.5 Die Hyperbel
|

  
|
Wenn α > β (die Schnittebene ist zu zwei Mantellinien des Kegels parallel)
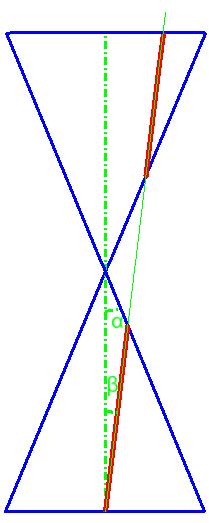
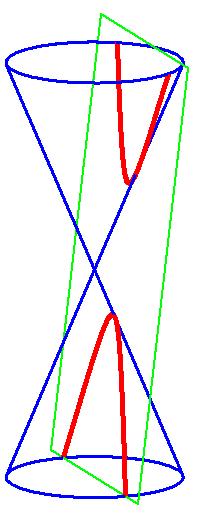
Definition
Die Hyperbel ist die Menge aller Punkte X, für die die Differenz der Abstände zu zwei festen Punkten - den Brennpunkten F1 und F2 - konstant ist.
hyp = {X | |F1X - F2X| = 2a}
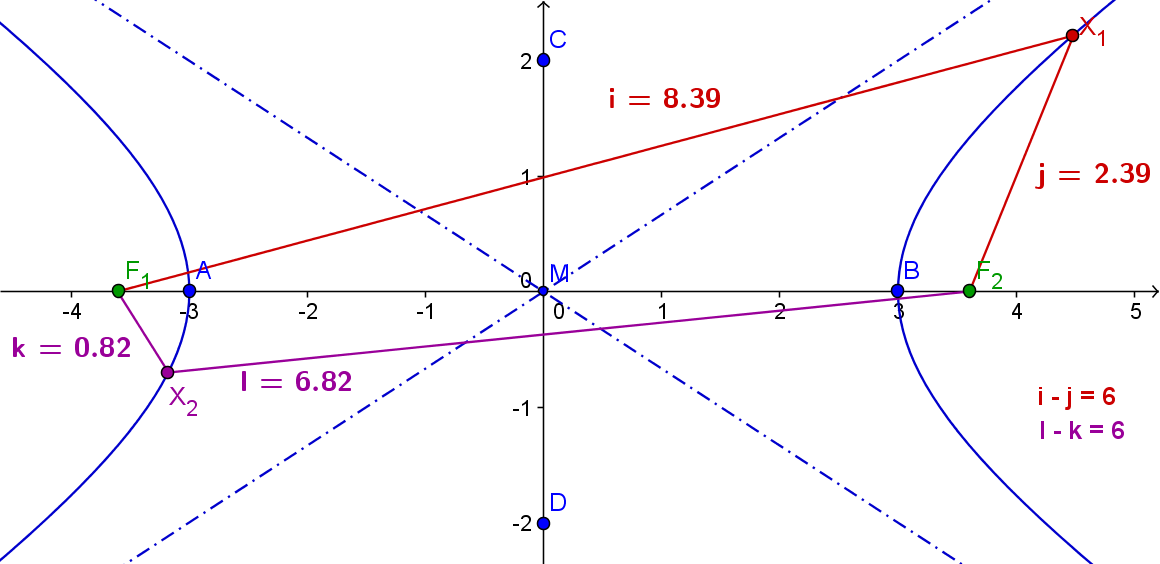
A, B . . . Hauptscheitel
C, D . . . Nebenscheitel
M . . . Mittelpunkt
F1, F2 . . . Brennpunkte
Hauptlagen der Hyperbel
Es gibt 2 verschiedene Hauptlagen der Hyperbel.
1.Hauptlage: Die Hauptachse liegt auf der x-Achse.
Die Gleichung der Hyperbel lautet: x²/a²- y²/b² = 1.
Die Gleichungen der beiden Asymptoten u und v lauten: u: y = x·b/a
v: y = -x·b/a
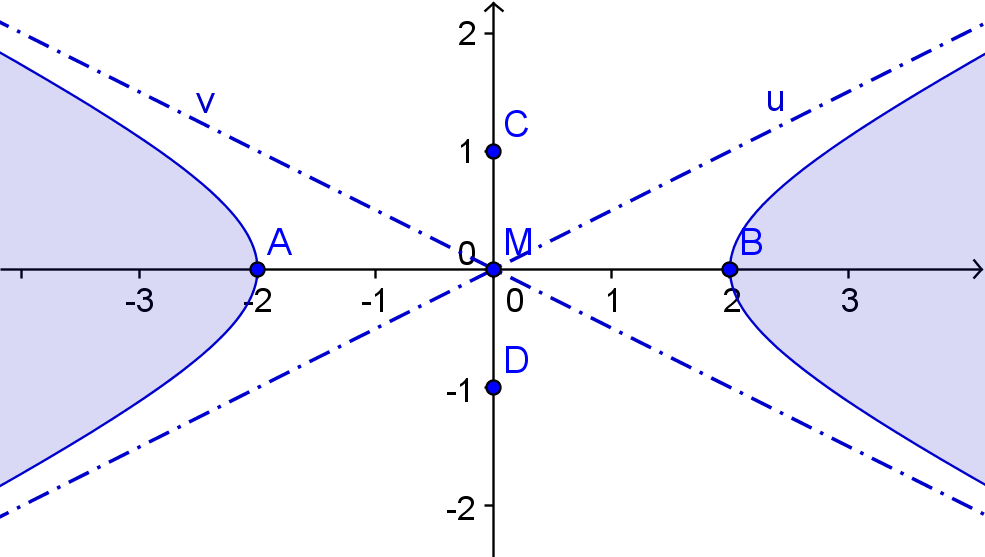
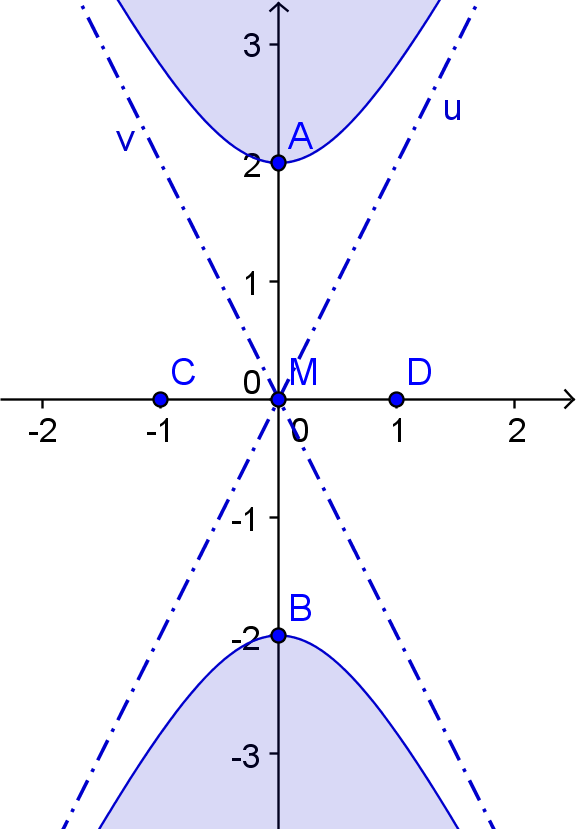
2.Hauptlage: Die Hauptachse liegt auf der y-Achse.
Die Gleichung der Hyperbel lautet: -x²/b² + y²/a² = 1.
Die Gleichungen der beiden Asymptoten u und v lauten: u: x = y·b/a
v: x = -y·b/a
–––––––––––––––––––––––––––––
Aufgabe:
Schreibe die Formel der Hyperbel in dein Schulübungsheft.
Versuche Skizzen der Hyperbel der 2 Hauptlagen in dein Heft zu zeichnen und schreibe die Formlen der Hyperbel und der Asymptoten dazu.
Der folgende Link öffnet eine GeoGebra-Datei in der eine Hyperbel mit Schieberegler ist.
Bewege sie und schreibe dir die Veränderungen der Hyperbel und der Asymptoten in dein Heft.
Was passiert mit der Hyperbel und den Asymptoten, wenn a = 0 oder b = 0?
In welchem Winkel stehen die Asymptoten zueinander, wenn a = b ist?
Hyperbel mit Schieberegler
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



