|
2.2 Strichliste
|

 

|
Strichliste
Mit Hilfe einer Strichliste kann man die Häufigkeit des Auftretens bestimmter Merkmale,
Ereignisse, Daten, usw. abzählen.
Schon in der Steinzeit, lange vor Erfindung der Schrift, wurden Anzahlen in Form von strichartigen Kerben markiert (z.B. Kerbholz).
Bei einer Datenerhebung können mittels Strichliste Ereignisse oder Merkmale geählt
werden. Für jedes Auftreten wird beim entsprechenden Eintrag auf der Liste ein vertikaler Strich gesetzt. Dabei ist es üblich, dass jeder fünfte Strich
horizontal gezeichnet wird und die letzten vier Striche durchstreicht. Durch die so gebildeten Fünfergruppen wird die Übersichtlichkeit beim Auswerten
gesteigert.
|
|
2.3 Häufigkeiten
|

  
|
Häufigkeiten
Unter Häufigkeit versteht man die Anzahl von Ereignissen/Werten/Objekten in einem Zeitraum oder in einer Liste. Wir unterscheiden hier drei verschiedene
Häufigkeiten:
-
Absolute Häufigkeit
-
Relative Häufigkeit
-
Prozentuelle Häufigkeit
Absolute Häufigkeit:
Diesen Wert bekommt man z.B. durch das Abzählen der Striche einer Strichliste.
Relative Häufigkeit:
Diesen Wert errechnet man, indem man den Wert der absoluten Häufigkeit durch die gesamten Werte dividiert.
Prozentuelle Häufigkeit:
Ist die relative Häufigkeit in Prozent ausgedrückt.
Beispiel:
Welche Haarfarben kommen in der Schulklasse mit 30 Schülerinnen und Schülern vor? Zuerst werden alle Schülerinnen und Schüler nach ihrer Haarfarbe befragt, und anschließend wird eine Tabelle erstellt.
|
Haarfarbe
|
absolute Häufigkeit
|
relative Häufigkeit
|
prozentuelle Häufigkeit
|
|
xi
|
H(xi)
|
h(xi)
|
h(xi) * 100
|
|
schwarz
|
8
|
0,27
|
27 %
|
|
dunkelbraun
|
3
|
0,1
|
10 %
|
|
braun
|
6
|
0,2
|
2 %
|
|
dunkelblond
|
5
|
0,17
|
17 %
|
|
blond
|
7
|
0,23
|
23 %
|
|
rot
|
1
|
0,03
|
3 %
|
Lernstoff, Eintrag in das Übungsheft
|
|
2.4 Mittelwert, Modus, Median
|

  
|
Den Mittelwert, Modus und Median Song kannst du dir freiwillig anhören. :-)
Mittelwert
Der Mittelwert wird auch Durchschnitt oder arithmetisches Mittel genannt. Er wird berechnet indem man alle vorhandenen Werte addiert und die Summe dieser
Werte dann durch die Gesamtanzahl der Werte dividiert. In der Formel sind die einzelnen Werte als "x" (xi) definiert und die Gesamtzahl der Werte mit "n".
Formeln
:
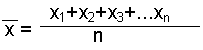 bzw. bzw. 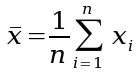
Beispiel:
Berechne den Mittelwert aus der folgenden Liste: {5, 9, 12, 1, 33, 14, 2, 10, 6, 8}
Berechnung: (5+9+12+1+33+14+2+10+6+8)/ 10 = 10
Median
Der Median ist der Wert, der in einer nach der Größe der Werte geordneten Liste genau in der Mitte liegt. Eine andere Bezeichnung wäre auch 'Zentralwert'.
Er ist unempfindlich gegenüber Ausreißern. Das bedeutet, dass bei der Liste die Werte folgendermaßen geordnet sind: {1, 2, 3, 5, 6, 7, 11, 14, 50,
60, 61, 62, 65, 67, 70}. Der Ausreißer in diesem Fall wäre die Zahl 50. Von 1 bis 14 steigen die Werte einigermaßen gleichmäßig an. Ebenso von 60 bis 70.
Aber von 14 auf 50 gibt es einen größeren Sprung und auch von 50 auf 60. Der Median in diesem Beispiel wäre die Zahl 14. Links und rechts
davon befinden sich jeweils sieben weitere Zahlen.
Bei einer exakten symmetrischen Verteilung entspricht der Median dem Mittelwert. Zum Beispiel bei dieser Werteliste: {2, 4, 6, 8, 10}. Der Median ist hier
die Zahl 6. Links und rechts von ihr befinden sich jeweils zwei weitere Zahlen. Wenn man den Mittelwert dazu berechnet bekommt man ebenfalls das Ergebnis
6. (Überprüfung mit der obigen Formel).
Es gibt zwei Fälle um den Median aus einer geordneten Liste zu berechnen:
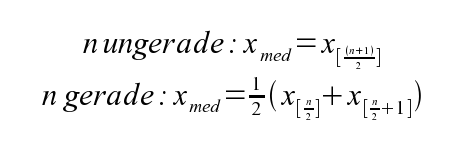
Fall 1:
ungerade Anzahl von Werten:
Hier geht man vor wie beim obigen Beispiel. Der Wert der in einer nach der Größe geordneten Liste genau in der Mitte ist, ist der Median. Bei einer sehr langen Liste ist es jedoch effizienter, wenn man die obige Formel verwendet.
Fall 2:
gerade Anzahl von Werten:
Hier gibt es zwei Werte die sich in der Mitte der Liste befinden. Um den Median nun zu berechnen addiert man die zwei in der Mitte liegenden Werte
miteinander und dividiert diese dann durch 2. Bei langen Listen empfiehlt sich wieder die obige Formel für die ungerade Anzahl an Werten.
Beispiel:
{1, 2, 3, 4, 5, 6} Die zwei Werte die genau in der Mitte liegen sind 3 und 4.
Berechnung:
. Also ist der Median in diesem Fall 3,5.
Modus
Der Modus oder auch Modalwert genannt, ist bei einer Liste von Messwerten, jener Wert, der am öftesten vor kommt.
Beispiel mit einem häufigsten Wert:
{1, 1, 1, 3, 3, 5, 5, 5, 5} Der Modus in diesem Fall ist der Wert 5 mit einer Häufigkeit von 4. (d.h. die Zahl 5 kommt vier Mal in der Liste vor).
Beispiel mit mehreren häufigen Werten:
{1, 1, 3, 3, 3, 4, 5, 5, 6, 6, 6} Die Häufigkeitsverteilung hat zwei Modi, 3 und 6, mit der Häufigkeit 3 (die Zahlen kommen jeweils drei Mal vor).
Beispiel ohne Modus:
{1, 4, 7, 9, 15} Da jeder Wert der Liste gleich oft vorkommt, gibt es in diesem Fall keinen Modus/ keinen Häufigsten Wert.
Lernstoff, Eintrag in das Übungsheft
|
|
2.5 Minimum, Maximum
|

 

|
Minimum, Maximum
Das Maximum ist der größte Wert in einer Liste.
Das Minimum ist der kleinste Wert in einer Liste.
Beispiel:
{5, 8, 2, 14, 3, 7, 26, 9}
Zuerst Liste ordnen: {2, 3, 5, 7, 8, 9, 14, 26}
dann sieht man sofort: Minimum = 2 und Maximum = 26
Lernstoff
|
|
2.6 Spannweite
|

 

|
Spannweite
Um die Spannweite zu erhalten, berechnet man die Differenz zwischen dem größten und dem kleinsten Wert einer Liste von Werten. Man Subtrahiert also
den kleinsten Wert vom größten. Ausreißer haben Einfluss auf die Spannweite.
Formel:
Maximum - Minimum = Spannweite
Beispiel (geordnete Liste):
{1, 2, 3, 4, 5, 70} Nun ist hier die Zahl 70 der Ausreißer. Wenn man nun den kleinsten Wert vom Größen abzieht erhält man
eine Spannweite von 69. Wie man sieht wirkt sie dieser Ausreißer sehr auf die Spannweite aus.
Lernstoff, Eintrag in das Übungsheft
|
|
2.7 Klasseneinteilung
|

 

|
Klasseneinteilung
Unter einer Klasseneinteilung versteht man, dass man Werte/Objekte/Daten nach ihren Merkmalsausprägungen zu 'Klassen' zusammenordnet.
Zum Beispiel
sind alle Schülerinnen und Schüler einer Schulklasse, die zwischen 150 cm und 160 cm groß sind in einer Klasse.
Durch das Einteilen in Klassen wird eine große Menge an Werten/Objekten/Daten auf eine Klasse verkleinert, damit verschiedene Untersuchungen einfacher
werden. Nachteil der Klasseneinteilung ist jedoch, dass auch Informationen verloren gehen. (Es werden keine Einzelwerte berücksichtigt.)
Man kann die Klassen auf zwei verschiedene Arte einteilen:
1. Möglichkeit:
|
Klasse 1
|
135 < 150 cm
|
|
Klasse 2
|
150 < 165 cm
|
|
Klasse 3
|
165 < 180 cm
|
|
Klasse 4
|
180 < 195 cm
|
Bei Klasse 1 gehören 135 cm und 150 cm nicht mehr zur Klasse weil die Klasse echt kleiner ist als 150 cm und echt größer als 135 cm ist. 135,1 cm und
149,9 cm sind noch in der Klasse.
2. Möglichkeit:
|
Klasse A
|
41 bis 50 kg
|
|
Klasse B
|
51 bis 60 kg
|
|
Klasse C
|
61 bis 70 kg
|
|
Klasse D
|
71 bis 80 kg
|
|
Klasse E
|
81 bis 90 kg
|
Hier sind bei der Klasse A die Werte 41 kg und 50 kg noch in der Klasse. Statt dem "bis" könnte man auch ein größ/kleiner-gleich-Zeichen einf/uumlgen. Die Anfangs und Endwerte der Klasse sind alle immer dabei.
Lernstoff, Eintrag in das Übungsheft
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



