(1) Potenzen mit gleicher Basis werden multipliziert, indem man die Basis mit der Summe der Exponenten potenziert:

www.quizlet.com
wobei a eine reelle Zahl ist und m,n aus den natürlichen Zahlen stammen.
(2) Potenzen mit gleicher Basis werden dividiert, indem man die Basis
mit der Differenz der Exponenten potenziert.

www.dieter-heidorn.de
wobei a eine reelle Zahl ist, die ungleich Null ist und m,n aus den natürlichen Zahlen stammen.
(3) Potenzen mit gleichem Exponenten werden multipliiziert, indem man das Produkt der Basen
mit dieser Hochzahl potenziert.

www.echteinfach.tv
wobei a,b reelle Zahlen sind und n aus den natürlichen Zahlen stammt
(4) Potenzen mit gleichem Exponenten werden dividiert, indem man den Quotienten der Basen
mit dieser Hochzahl potenziert.

www.mathematik.net
wobei a,b reelle Zahlen sind, mit b ist ungleich Null und n aus den natürlichen Zahlen stammt.
(5) Potenzen werden potenziert, indem man die Basis mit dem Produkt der Exponenten potenziert.
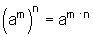
www.brinkmann-du.de
wobei a eine reelle Zahl ist und m,n aus den natürlichen Zahlen stammen.
Lernstoff
|



