Bisher haben wir genau genommen nur über Rechenregeln gesprochen. Nun wollen wir uns
zum ersten Mal einer "richtigen" mathematischen Problemstellung zuwenden. Betrachten wir
eine positive reelle Zahl. Gibt es eine reelle Zahl, deren Quadrat gleich der gegebenen Zahl ist?
Aus Beobachtung wissen wir schon, dass:
3
2 = 3 · 3 = 9
4
2 = 4 · 4 = 16
5
2 = 5 · 5 = 25
Weiters haben wir auch schon in der Geometrie die Quadratwurzel gezogen. Wenn wir jetzt nochmal auf unsere Beobachtung oben schauen und unser Wissen über Quadratwurzeln berücksichtigen, können wir erkennen, dass es einen Zusammenhang gibt:
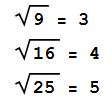
Also haben wir eine Antwort zu unserer Frage gefunden:
Ja es gibt eine positive reelle Zahl(3) deren Quadrat die Zahl gegebene Zahl 9 ergibt. 3
2 = 9
Es gibt aber auch noch einige andere Zahlenpaare, die wir für die Beantwortung unserer Frage heranziehen könnten (siehe oben).
Wir haben aber auch gesehen, dass:

daraus vermuten wir einen Zusammenhang von Quadratwurzeln und x
2.



