|
1.1 Unvollkommenheit der Reellen Zahlen
|

 

|
Viele quadratische Gleichungen der Form ax2 + bx + c = 0 (mit a,b aus den reellen Zahlen und a ¹ 0), sind in den reellen Zahlen lösbar.
Doch es gibt auch solche, die nicht lösbar sind, wie z.B. x2 = -1, denn Quadrate reeller Zahlen sind nie negativ.
Jedoch besitzt z.B. die Gleichung 4x = 5 in den ganzen Zahlen auch keine Lösung, doch durch die Erweiterung von den ganzen Zahlen zu den rationalen Zahlen wird sie lösbar.
Daher liegt die Frage nahe, ob die reellen Zahlen nicht auch so erweitert werden kann, dass alle quadratischen Gleichungen lösbar werden.

Diese Abbildung zeigt die Ober- und Unterordnungen der verschiedenen Zahlenmengen
|
|
1.2 Leonhard Euler
|

 

|
Einer der ersten Mathematiker, der versuchte dieses Problem zu lösen, war Leonhard Euler (1707-1783). Dies gelang ihm durch Einführung einer neuen Zahl i.
|
|
1.3 Die imaginäre Zahl "i"
|

  
|
Die Einführung dieser neuen Zahl i sollte die Lösung der Gleichung x2 = -1 sein. Daher sollte gelten:
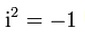
i wird hierbei als imaginäre Einheit bezeichnet.
Durch multiplikative Verknüpfung reeller Zahlen b mit der imaginären Einheit i entstanden dann die "Imaginärzahlen" bi. Mit diesen wird so gerechnet, als ob i eine durch eine Variable vertretene reelle Zahl wäre.
(Beispiel: 2i + 3i = 5i)
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



