|
4.1 Rechnen mit komplexen Zahlen
|

 

|
Komplexe Zahlen werden meist in der Form dargestellt, wobei und reelle Zahlen sind und die imaginäre Einheit ist. Auf die so dargestellten komplexen Zahlen lassen sich die üblichen Rechenregeln für reelle Zahlen anwenden, wobei stets durch −1 ersetzt werden kann und umgekehrt.
|
|
4.2 Addition
|

  
|
Für die Addition zweier komplexer Zahlen a+bi und c+di gilt:

|
|
4.3 Subtraktion
|

  
|
Analog zur Addition (siehe oben) funktioniert auch die Subtraktion:

|
|
4.4 Multiplikation
|

  
|
Für die Multiplikation gilt entsprechend

Diese Formel ergibt sich mit der Definition durch einfaches Aus-multiplizieren und Neugruppieren.
|
|
4.5 Division
|

  
|
Der Quotient zweier komplexer Zahlen a + bi und c + di mit c + di¹ 0 lassen sich berechnen, indem man den Bruch mit der zum Nenner c+di konjugiert komplexen Zahl c - di erweitert.
Der Nenner wird dadurch reell (und ist gerade das Quadrat des Betrages von c+di):

|
|
4.6 Rechenbeispiele für die vier Grundrechnungsarten
|

 

|
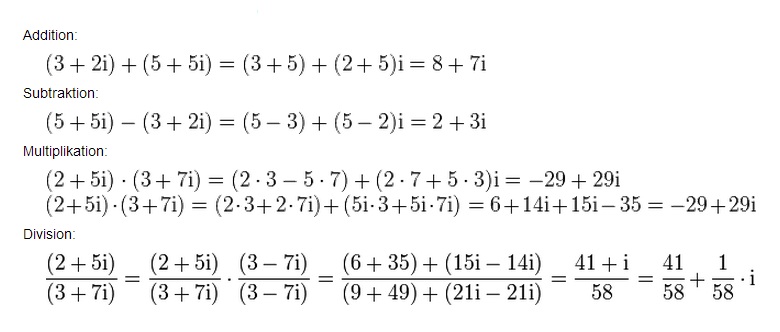
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



