|
5.1 Zusammenfassung
|
|
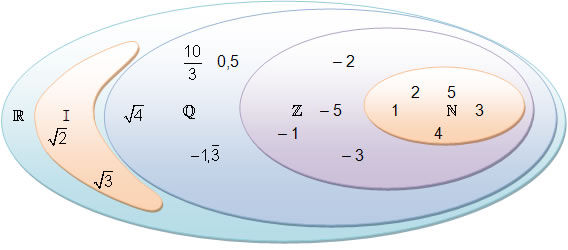Im Zuge der Behandlung unterschiedlicher Zahlenmengen haben wir die natürlichen Zahlen sukzessive bis hin zu den reellen Zahlen erweitert.
Dabei gilt folgende Beziehung: ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ.
Die rationalen Zahlen ℚ liegen dicht auf der Zahlengerade, d.h. zwischen zwei beliebigen rationale Zahlen lässt sich immer eine weitere rationale Zahl finden.
Obwohl ℚ dicht ist, bleiben doch Lücken auf der Zahlengerade bestehen. Erst die reellen Zahlen umfassen den Zahlenstrahl komplett, man sagt ℝ ist vollständig.
Nicht alle Rechenoperationen sind in allen Mengen unbeschränkt ausführbar. Manche können aus der Menge herausführen.
Im Folgenden werden die in den unterschiedlichen Zahlenmengen stets ausführbaren Operationen aufgelistet:
ℕ: Addition, Multiplikation
ℤ: Addition, Multiplikation, Subtraktion
ℚ: Addition, Multiplikation, Subtraktion, Division (außer durch Null)
ℝ: Addition, Multiplikation, Subtraktion, Division (außer durch Null)
|
|
5.3 Ausblick
|
|
Die schrittweise Vervollständigung der Zahlenmengen hat letztendlich zur Menge ℝ der reellen Zahlen geführt, welche die Zahlengerade vollständig ausfüllen.
Da jeder Punkt der Zahlengerade einer reellen Zahl entspricht, könnte die Vermutung aufkommen, damit wären bereits alle Zahlen erfasst.
Diese Vermutung ist jedoch falsch!
So lassen sich einige mathematische Operationen in ℝ nicht durchführen.
Die einfache mathematische Gleichung x²+1=0 führt etwa durch Umformung zur Gleichung x=√-1, die jedoch in ℝ keine Lösung besitzt.
Um auch Wurzeln aus negativen Zahlen ziehen zu können, muss ℝ zu den sogenannten komplexen Zahlen ℂ erweitert werden.
In dieser Zahlenmenge ℂ hat die Gleichung x = √-1 dann zwei verschiedene Lösungen: x1=+i, x2=-i, wobei i die imaginäre Einheit bezeichnet.
Veranschaulichen lassen sich diese komplexen Zahlen im Allgemeinen nicht mehr auf dem ein-dimensionalen Zahlenstrahl.
Die komplexen Zahlen sind vielmehr Punkte auf einer zwei-dimensionalen Zahlenebene.
Mehr dazu erfährst du in der 7.Klasse, wo die komplexen Zahlen ausführlicher behandelt werden...
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|
