|
1.1 Die Trigonometrie - Einleitung
|

 

|
Was bedeutet das Wort Trigonometrie und mit welchem Gebiet beschäftigt sich die Trigonometrie?
Eine kleine Wortkunde:
- tri bedeutet 'drei' Beispiel: Triathlon, . . .
- gon bedeutet 'Winkel'/'Eck' Beispiel: Pentagon – das Fünfeck mit 5 Winkeln
- metrie bedeutet 'Messung' Beispiel: Geometrie – die Erdvermessung
|
 |
 |
 |
Das Wort impliziert also die 'Dreiwinkelmessung' oder allgemein die 'Dreiecksberechnung'. Während die Planimetrie die Konstruktion eines Dreieckes aus gegebenen Stücken lehrt,
bei der die Genauigkeit der Resultate verhältnismäßig gering ist, liefert die Trigonometrie auf rechnerischem Weg exaktere Ergebnisse.
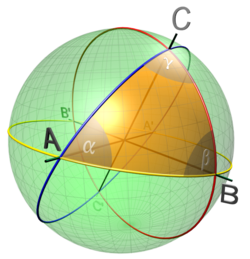
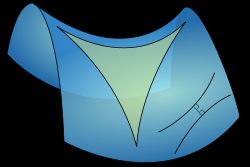
Soweit Fragestellungen der ebenen Geometrie trigonometrisch behandelt werden, spricht man von ebener Trigonometrie; daneben gibt es die sphärische Trigonometrie, die sich mit Kugeldreiecken (sphärischen Dreiecken) befasst, und die hyperbolische Trigonometrie.
Im Folgenden gilt als Einführung in die Trigonometrie, einen Überblick über die ebene Geometrie zu erlangen. Die Grundaufgabe der Trigonometrie besteht darin, aus drei Größen eines gegebenen Dreiecks (Seitenlängen, Winkelgrößen, usw.) andere Größen dieses Dreiecks zu berechnen.
Als Hilfsmittel werden die trigonometrischen Funktionen (hier: Winkelfunktionen) sin (Sinus), cos (Kosinus), tan (Tangens) verwendet.
Lernstoff
|
|
1.2 Zusatz: Strahlensätze
|

 

|
Die Strahlensätze werden dazu benötigt um gewisse Beziehung, oder Verhältnisse von Strecken auszudrücken. Wiederhole diese um einen noch besseren Überblick im nächsten Kapitel zu erlangen.
Durchforste deine bisherigen Lernmaterialen nach den Strahlensätze. In welchem Zusammenhang hast du sie bis jetzt kennengelernt?
Versuche diese Zuordnungsübung, und schaue ob du dich noch an die Strahlensätze erinnern kannst.
Achtung, die Zeit läuft mit!
Viel Spass dabei!
Wiederholung
|
|
1.3 Sinus, Cosinus und Tangens - Einleitung
|

  
|
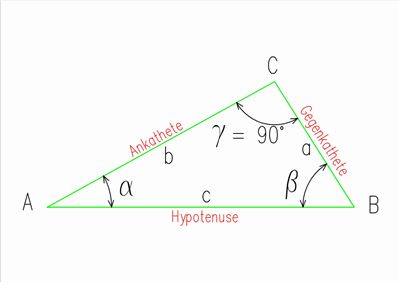
Um die trigonometrischen Funktionen sin, cos und tan verstehen zu lernen ist es hilfreich zuvor ein rechtwinkeliges Dreieck zu betrachten.
In einem rechtwinkeligen Dreieck ABC seien a und b die Katheten, c die Hypothenuse, die spitzen Winkel entsprechend α und β, wobei gilt α + β = 90°. Man nennt a die Gegenkathete und b die Ankathete des Winkels α.
RECHTWINKELIGES DREIECK
Zieht man in einem rechtwinkeligen Dreieck ABC zur Kathete a Parallelen wie B1C1 und B2C2, so entstehen rechtwinkelige Dreiecke AB1C1 und AB2C2.
Daraus folgt (mittels Strahlensätze!): a ⁄ c = a1 ⁄ c1 = a2 ⁄ c2
Da durch das Verhältnis zweier Seiten das rechtwinklige Dreieck in der Gestalt festgelegt ist, ist auch die Größe des Winkels α (und damit auch β) eindeutig bestimmt. Umgekehrt ist das Seitenverhältnis im rechtwinkligen Dreieck durch den Winkel α bestimmt. Man bezeichnet ein solches Streckenverhältnis als eine Funkton des Winkels α und zwar als trigonometrische Funktion von α. Dadurch ist die Möglichkeit gegeben, gesuchte Winkel durch Streckenverhältnisse auszudrücken. Auf diese Weise kommt man über die metrische Geometrie der Ebene, die hauptsächlich nur Beziehungen zwischen Strecken kennt (u.a. Pythagoras), hinaus zur Trigonometrie als neues Wissenswerkzeug.
| Defintion der trigonometrischen Funktionen: |
 |
 |
Arbeitsmaterialien und Arbeitsaufträge:
- Aufgabe bis zur nächsten Unterrichtseinheit: Aufgabe I
- Folgende Software wirst du in den nächsten Unterrichtseinheiten benötigen: GeoGebra Lade diese Software herunter und probiere ein rechtwinkeliges Dreieck zu zeichnen (vgl. Grafik oben).
Wiederholung, Lernstoff
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



