|
1.1 Polarkoordinaten eines Punktes
|

 
|
Um die Lage eines Punktes P in einem Koordinatensystem zu beschreiben gibt es zwei Möglichkeiten:
1.) Kartesische Koordinaten: P(x/y) (diese Methode ist uns bereits bekannt!)
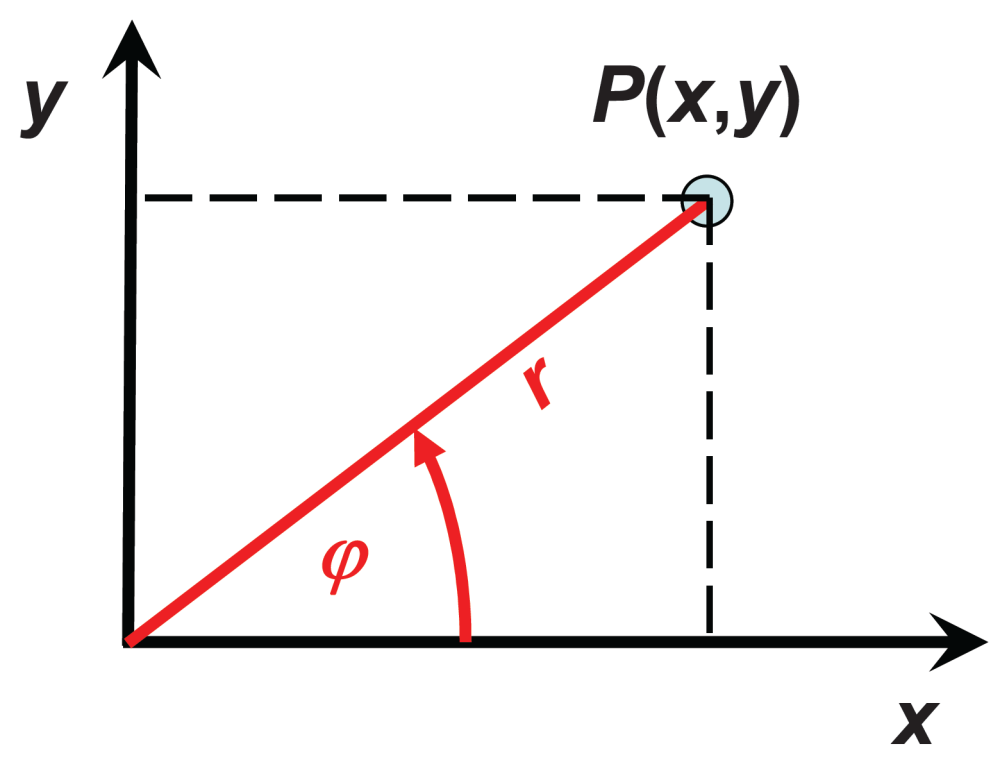
2.) Polarkoordinaten: P[r;φ] (damit werden wir uns nun beschäftigen)
r...Radius
φ...Winkel (wobei φ zwischen 0° und 360° liegt und immer gegen den Uhrzeigersinn gelesen wird)
|
|
1.2 Übungen zu Polarkoordinaten
|

 

|
Zeichne folgenden Punkte in ein Koordinatensystem und lies die jeweiligen kartesischen Koordinaten ab:
a) P [4; 60°]
b) Q [3; 320°]
c) R [6; 175°]
d) S [5; 230°]
Hausübungsheft
|
|
1.3 Einheitskreis
|

 
|
Der Einheitskreis hat den Mittelpunkt O (0/0) und den Radius r=1
Interessante Punkte am Einheitskreis:
Der y-Wert (y(φ)) des Winkels φ = 0° beträgt 0
Der y-Wert (y(φ)) des Winkels φ = 90° beträgt 1
Der y-Wert (y(φ)) des Winkels φ = 180° beträgt 0
Der y-Wert (y(φ)) des Winkels φ = 270° beträgt -1
Die y-Werte der Winkel zwischen 0° und 180° sind positiv
Die y-Werte der Winkel zwischen 180° und 360° sind negativ
Ein Punkt P bewegt sich am Einheitskreis zwischen -1≤y≤1
Die kartesischen Koordinaten eines Punktes P hängen von φ ab.
Wir definieren :
sin φ ... y-Koordinate von P
cos φ ... x-Koordinate von P
Für jeden Winkel φ Element aus [0° 360°] gilt: (sin φ)2 + (cos φ)2 = 1
Vorzeichen von Sinus und Cosinus am Einheitskreis:
φ _______________ sin φ _______cos φ
0° < φ < 90°_______ + __________ +
90° < φ < 180°_____ + __________ -
180° < φ < 270°_____ - __________ -
270° < φ < 360°_____ - __________ +
|
|
1.4 Übungen Einheitskreis
|

 

|
Zeichne den Winkel φ in einem Einheitskreis mit dem Radius r=1 dm ein und lies danach sin φ und cos φ ab. Überprüfe anschließend(!) deine Werte mit dem Taschenrechner.
a.) φ = 190°
b.) φ = 215°
c.) φ = 30°
d.) φ = 120°
e.) φ = 90°
f.) φ = 355°
g.) φ = 60°
h.) φ = 45°
Hausübungsheft
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



