|
3.1 Sinussatz
|

 
|
Wann wird der Sinussatz eingesetzt?
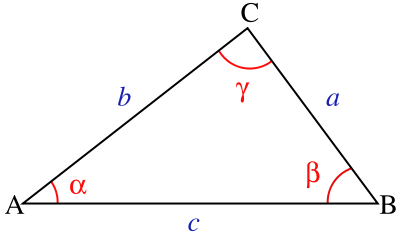
* um ein allgemeines Dreieck aufzulösen
* wenn man eine Seite und zwei Winkel kennt
* wenn man zwei Seiten und einen Winkel, der von diesen nicht eingeschlossen ist, kennt.
Sinussatz:
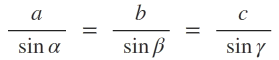
|
|
3.2 Ausführung Sinussatz
|

 
|
Gegeben: a = 7, b = 6, α = 60°
a / sinα = b / sinβ →
sinβ/b = sinα / a →
sinβ = (b*sinα) / β →
sinβ = (6*sin60°) / 7 →
sin-1((6*sin60°) / 7) →
β ≈ 47,93°
Gegeben: α = 65,8°, c = 14cm, γ = 80°
a/sinα = c/sinγ →
a = (c*sinα) / sinγ →
a = (14*sin65,8°) / sin80° →
sin-1 = (14*sin65,8°) / sin80° →
a ≈ 12,79 cm
|
|
3.3 Übungen Sinussatz
|

 

|
Berechne die fehlenden Seiten und Winkel der Dreiecks.
Mach jedoch davor eine Skizze!
a.) b = 6 cm, c = 8 cm, γ = 75°
b.) b = 7,9 cm, c = β = 52°
c.) a = 7 cm, c = 4 cm, α = 80°
d.) b = 11 cm, α = 25°, γ = 45°
e.) c = 6,9 cm, α = 55°, β = 45°
f.) b = 6,1 cm, β = 15°, γ = 140°
Hausübungsheft
|
|
3.4 Cosinussatz
|

 
|
Wann wird der Cosinussatz eingesetzt?
* um ein allgemeines Dreieck aufzulösen
* wenn man drei Seiten kennt
* wenn man zwei Seiten und den eingeschlossenen Winkel kennt
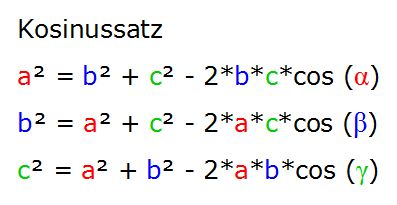

|
|
3.5 Ausführung Cosinussatz
|

 
|
Gegeben: a = 19 cm, b = 12 cm, γ = 123°
c2 = a2 + b2 - 2*a*b*cosγ
c2 = 192 + 122 - 2*19*12*cos123°
c ≈ 2,74
Gegeben: a =12 cm, b = 9 cm, c = 4 cm
cosα = (b2 + c2 - a2) / 2*b*c
cosα = (92 + 42 - 122) / 2*9*4
α = cos-1; ((92 + 42 - 122) / 2*9*4)
α ≈ 130,75°
|
|
3.6 Übungen Cosinussatz
|

 

|
Berechne mit Hilfe des Cosinus-Satzes und des Sinus-Satzes die fehlenden Seitenlängen und Winkel.
a.) a = 3 cm, b = 5 cm, γ = 55°
b.) b = 7,2 cm, c = 6 cm, α = 52°
c.) a = 7,9 cm , b = 10, 8 cm, c = 15 cm
d.) b = 12,3 cm, c = 7,4 cm, �B1 = 21°
e.) a = 4,9 cm, b = 9,6 cm, c = 5,3 cm
Hausübungsheft
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



