|
2.1 Wiederholung der Satzgruppe von Pythagoras
|

 
|
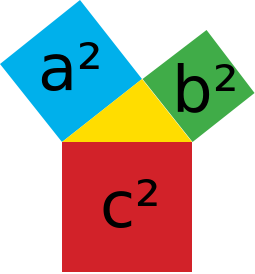
Es seien a,b,c die Seiten des Dreiecks, wobei c = Hypotenuse
a2 + b2 = c2
Die Umformung nach a2 und b2 sei dir selbst überlassen.
Falls du vergessen hast, wie man die gesuchten Seite berechnen kann, schau in deinem Übungsheft nach und mach zur Sicherheit die Übungen aus Punkt 2.2
|
|
2.2 Übungen zu Satzgruppe von Pythagoras
|

 

|
Berechne die fehlende Seite
a.) a = 3, b = 4, c =?
b.) b = 21, c = 29, a = ?
c.) c = 19, a = 17, b = ?
d.) a = 5cm, c = 10cm, b = ?
e.) a = 24cm, b = 7cm, c = ?
|
|
2.3 Sinus un Cosinus im rechtwinkeligen Dreieck
|

 
|
Wie wir bereits wissen beträgt die Winkelsumme in einem Dreieck 180°
Das rechtwinkelige Dreieck ist ein Spezialfall, denn es besitzt genau einen Winkel, der 90° beträgt. Die anderen beiden Winkel können somit gemeinsam nur noch 90° ausmachen.
Die Hypotenuse ist die längste Seite in einem rechtwinkeligen Dreieck und liegt immer gegenüber des rechten Winkels
Die Ankathete schließt gemeinsam mit der Hypotenuse den Winkel α ein.
Die Gegenkathete liegt gegenüber des Winkels α.

Für jeden Winkel φ mit 0° < φ < 90° gilt:
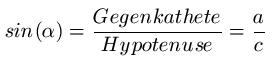
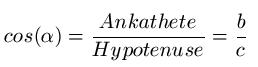
Anmerkung: In unserem Fall ist α = φ !
|
|
2.6 Tangens
|

 
|
Die Steigung k = ∆ y / ∆ x
Wenn wir nun ∆ y als sin φ und ∆ x als cos φ betrachten fällt uns die folgende Definition nicht schwer zu verstehen:
Der Tangens eines Winkes beschreibt die Steigung des Winkelschenkels:
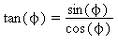
Beachte dabei dass dies nicht für φ = 90° und φ = 270° gilt!
|
|
2.7 Tangens und Cotangens im rechtwinkeligen Dreieck
|

 
|
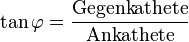
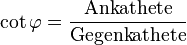
|
|
2.8 Übungen zu Sinus und Cosinus im rechtwinkeligen Dreieck
|

 

|
Mach zu jedem Beispiel eine Skizze und markiere alle Größen die bereits gegeben sind.
Berechne danach die fehlenden Seitenlängen und Winkel
a.) a = 8cm, c = 9cm, γ = 90°
b.) c = 10cm, β = 90°, γ = 60°
c.) a = 3cm, α = 30°, γ = 90°
d.) b = 9cm, α = 73°, γ = 90°
e.) a = 2,7cm, b = 4,4cm, β = 90°
Hausübungsheft
|
|
2.9 Übungen zu Tangens und Cotangens im rechtwinkeligen Dreieck
|

 

|
Mach zu jedem Beispiel eine Skizze und markiere alle Größen die bereits gegeben sind.
Berechne danach die fehlenden Seitenlängen und Winkel
a.) a = 6,3cm, b = 7,8cm, γ = 90°
b.) c = 4,2cm, α = 60°, β = 90°
c.) a = 7,2cm, α = 30,2°, γ = 90°
d.) b = 11,1cm, α = 90°, γ = 15°
e.) a = 3,6cm, c = 8,8cm, γ = 90°
Hausübungsheft
|
|
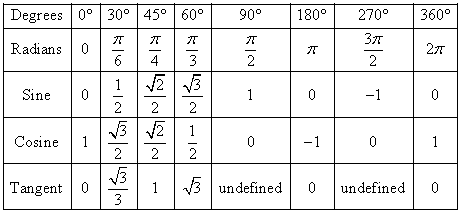
2.11 Werte für spezielle Winkel
|

 
|
Erklärung zu dieser Tabelle:
degrees = Grad, sine = Sinus, cosine = Cosinus
Die Werte für "radians" und "tangent" musst du dir nicht auswendig merken.
Jedoch mit den Werten für Sinus und Cosinus solltest du sehr vertraut sein!
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



