|
3.1 Das allgemeine Viereck
|

 


|
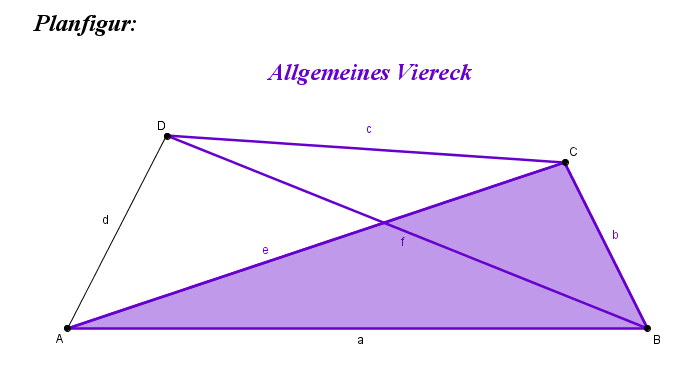
Eine durch vier Strecken eingeschlossenen Figur wird als allgemeines Viereck bezeichnet.
Alle Seiten sind verschieden lang.
Alle Winkel sind verschieden groß.



Eintrag in dein Lerntagebuch
|
|
3.2 Das Rechteck
|

 


|
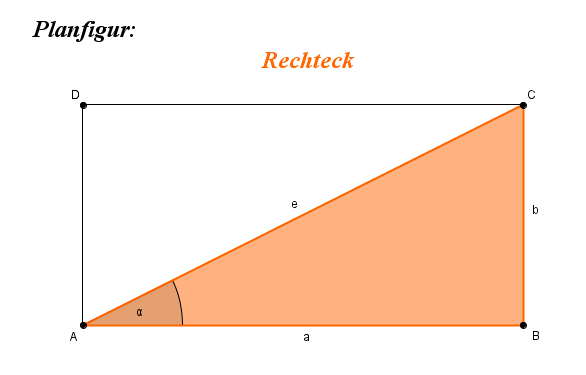
Ein Viereck, welches vier gleich große (Innen-)Winkel (90°, siehe rechter Winkel) hat, ist ein Rechteck.
Die Diagonalen sind gleich lang und halbieren sich gegenseitig.



Eintrag in dein Lerntagebuch
|
|
3.3 Das Quadrat
|

 


|
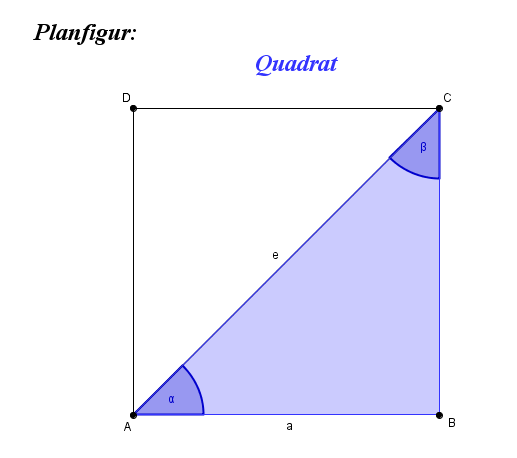
Das regelmäßige Viereck wird auch als Quadrat bezeichnet.
Es besitzt 4 gleich lange Seiten und auch vier gleich große (Innen-)Winkel (90°).
Die Diagonalen (e,f) sind gleich lang und halbieren sich gegenseitig.
Die Diagonalen stehen senkrecht aufeinander und bilden Symmetrieachsen.



Eintrag in dein Lerntagebuch
|
|
3.4 Das Trapez
|

 


|
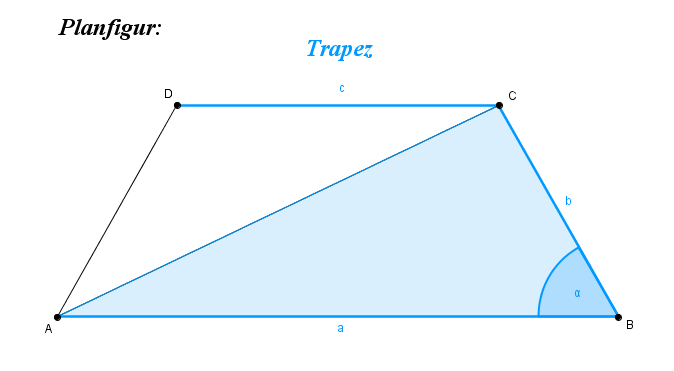
Ein Trapez ist ein Viereck mit mindestens zwei parallelen Seiten.



Eintrag in dein Lerntagebuch
|
|
3.5 Das Parallelogramm
|

 


|
Sind je zwei einander gegenüberliegende Seiten parallel, spricht man vom Parallelogramm.
Die jeweils gegenüberliegenden Seiten und Winkel sind gleich groß.
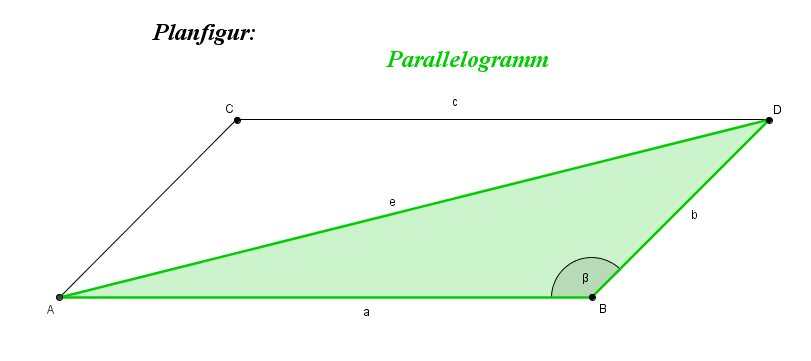
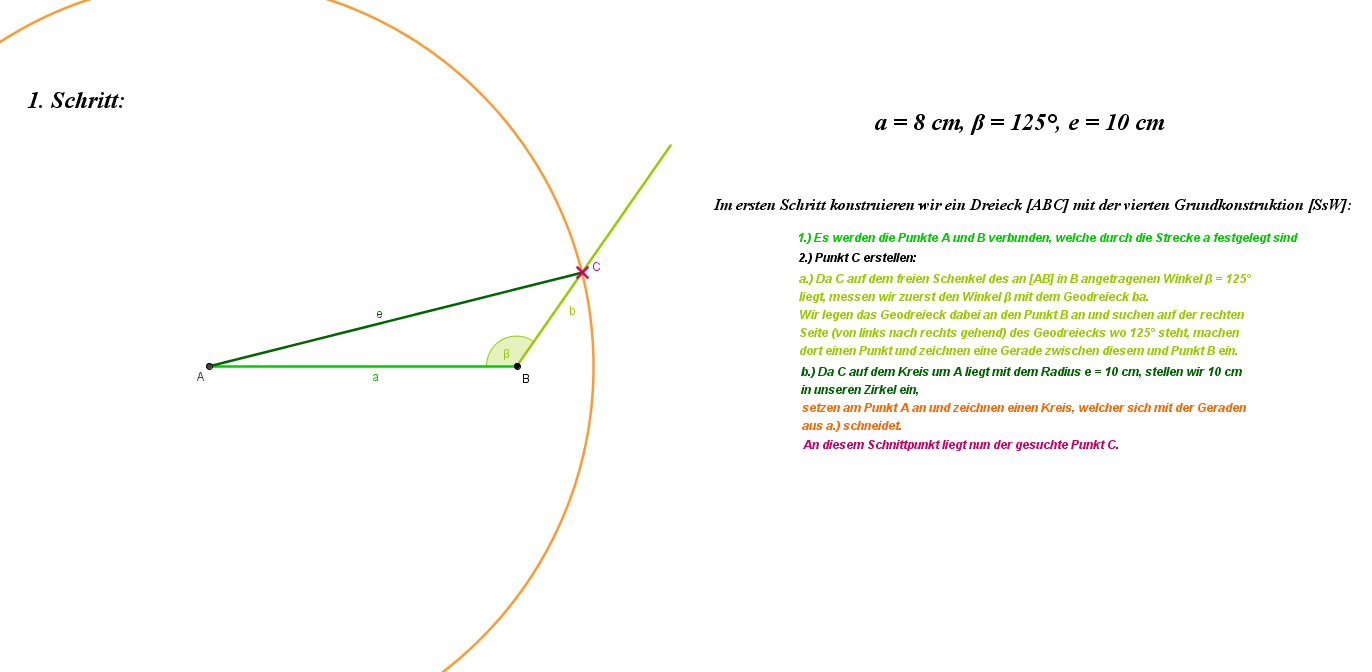
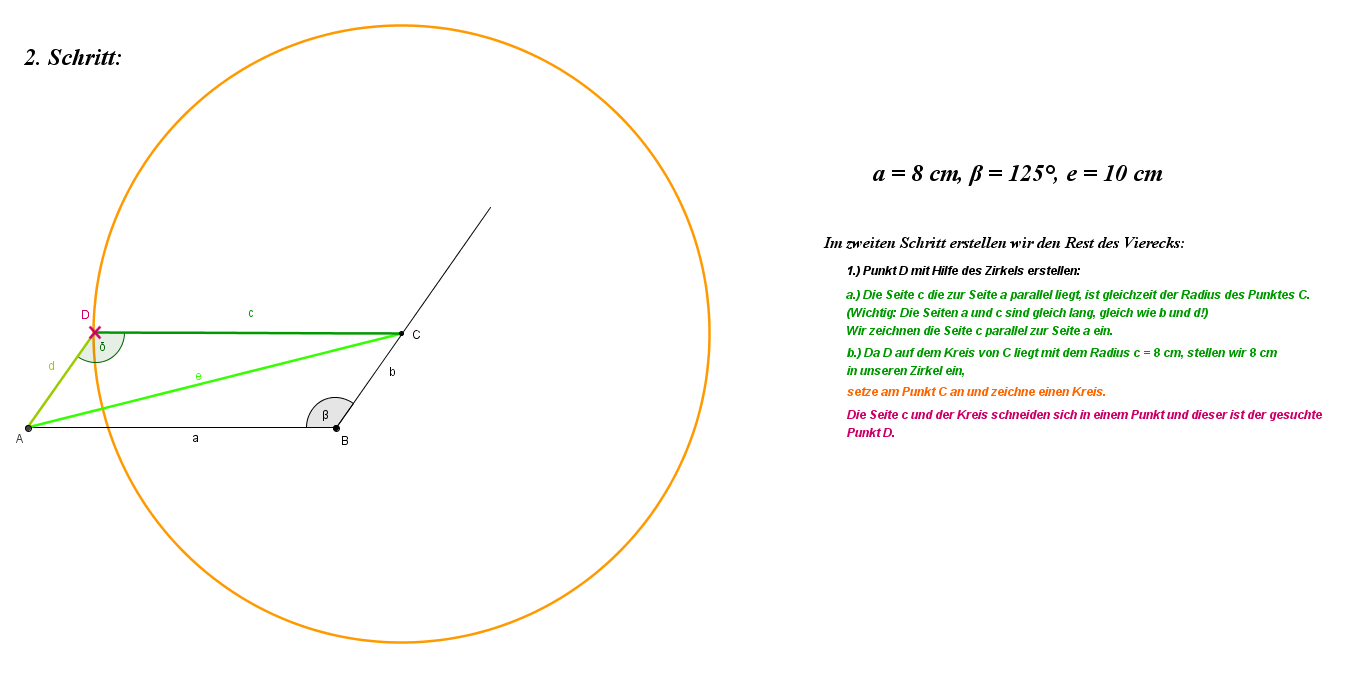
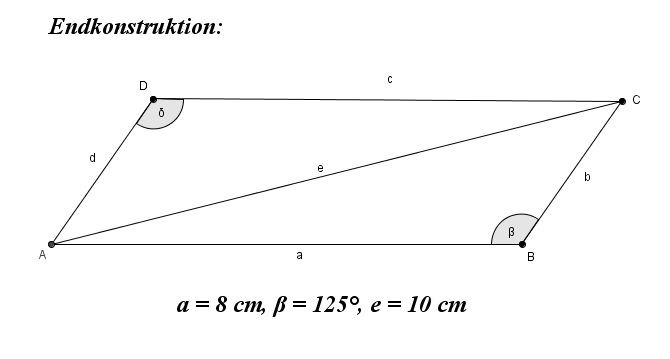
Eintrag in dein Lerntagebuch
|
|
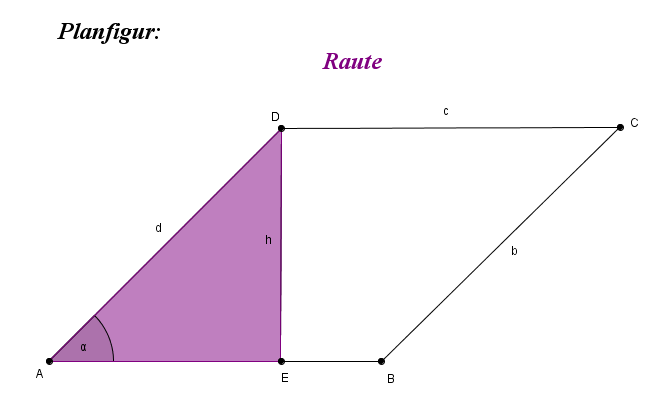
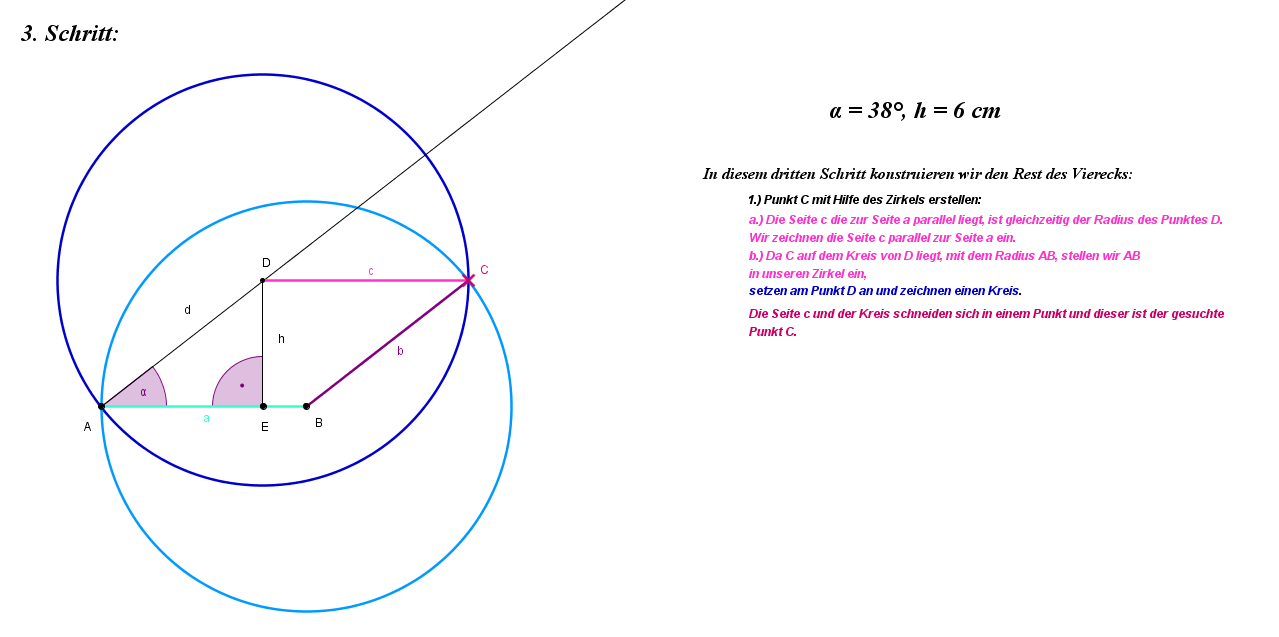
3.6 Die Raute
|

 


|
Bei vier gleich langen Seiten spricht man von einem Raute (Rhombus).
Die Diagonalen halbieren sich gegenseitig und stehen senkrecht aufeinander.
Beide Diagonalen bilden Symmetrieachsen.



Eintrag in dein Lerntagebuch
|
|
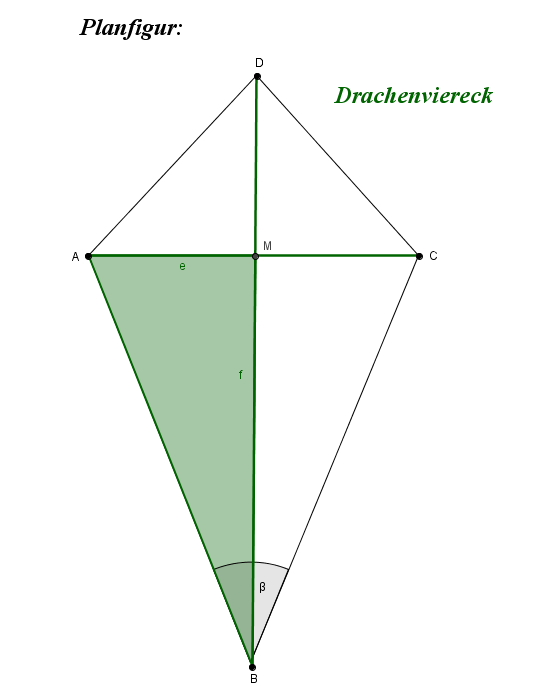
3.7 Das Deltoid
|

 


|
Beim Deltoid (Drachenviereck) stehen die Diagonalen senkrecht aufeinander, und eine Diagonale wird durch die andere halbiert.
Dies ist gleichbedeutend damit, dass es zwei Paare benachbarter Seiten gibt, die jeweils gleich lang sind.
Eine der Diagonalen bildet die Symmetrieachse.



Eintrag in dein Lerntagebuch
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



