|
4.1 Der Thaleskreis
|

 


|
In einem Thaleskreis können Dreiecke mit rechtem Winkel konstruiert werden, ohne dass man ein Geodreieck benötigt.
Mit dem Thaleskreis kann man auch Linien finden, die Kreise nur in einem bestimmten Punkt berühren und kann diese Punkte genau ausrechnen.
Eintrag in dein Lerntagebuch
|
|
4.2 Satz des Thales
|

 
|
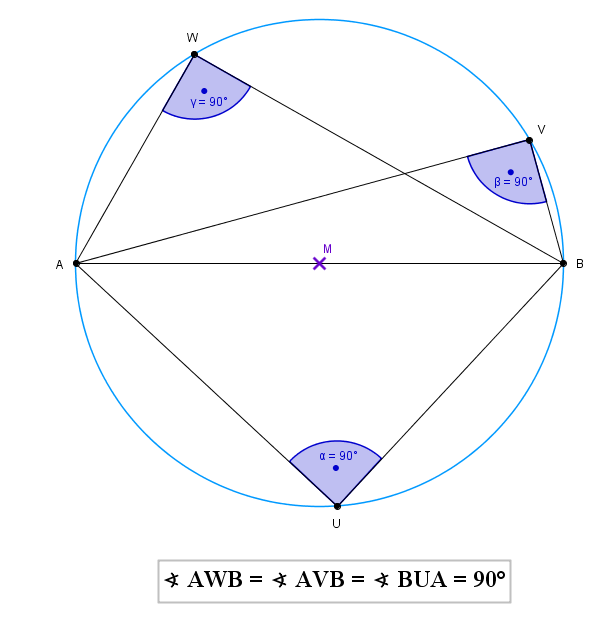
Er besagt, wenn man in den Thaleskreis Dreiecke zeichnet, so besitzen diese bei γ immer einem rechten Winkel.
Dies bedeutet, dass sich immer gegenüber unserer Strecke AB ein Winkel von 90° bildet.
|
|
4.3 Was besagt der Umfangswinkelsatz?
|

  

|
1.) All Umfangswinkel auf derselben Seite einer Sehne sind gleich groß
(Die Winkel müssen auf derselben Seite der Sehne liegen.).
2.) Der Mittelpunktswinkel ist doppelt so groß wie die zugehörigen Umfangswinkel.

Eintrag in dein Lerntagebuch
|
|
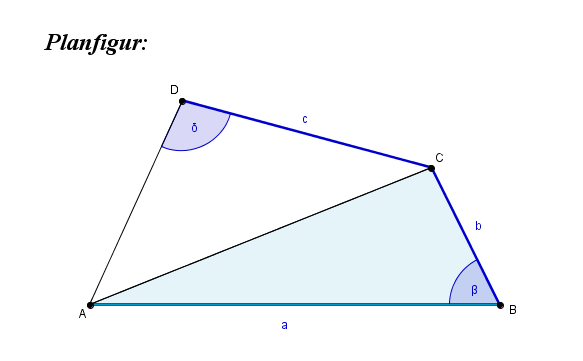
4.4 Beispiele zur Konstruktion mit Hilfe des Umfangswinkelsatzes
|

 

|



|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



