3.1 Ungleichungen
http://www.mathe-online.at/materialien/ppvo/files/ungleichungen-exkurs.html
|

 
|
Was ist eine Ungleichung?
Was muss man beim Rechnen mit Ungleichungen beachten?
Überlege zuerst und klick dann den obenstehenden Link an; dort findest du die Antworten auf diese Fragen.
Angenommen, du willst eine Ungleichung mit dem Term (x+5) multiplizieren oder dividieren. Was musst du beachten?
Die Antwort auf diese Frage kannst du im Kapitel Äquivalenzumformungen bei Ungleichungen hier nachschauen.
|
3.3 Ungleichungssystem mit UND verknüpft
http://www.mathe-online.at/materialien/ppvo/files/bsp_UND.htm
|

 
 
|
Ein Ungleichungssystem ist ein System, das aus mehreren Ungleichungen besteht:
(2x-5<7)Ù(-3x-1£-7)
Die Elemente der Lösungsmenge müssen sowohl die erste als auch die zweite Ungleichung erfüllen.
Versuche, die Lösungsmenge für das obige System zu finden.
Eine Musterlösung findest du im obigen Link. Überleg genau, warum die Gesamtlösung die DURCHSCHNITTSMENGE der beiden Lösungsmengen ist.
|
|
3.5 Fortlaufende Ungleichungen
|

 
|
Wie kann man aus der folgenden Ungleichung ein Ungleichungssystem erhalten und um welches handelt es sich?
-3<2x+1<5x-1
Freiwillig: Löse das Gleichungssystem!
|
|
3.6 Betragsungleichungen
|

 
|
Weißt du, was folgender Ausdruck bedeutet?
½-5½
Die Striche links und rechts von -5 nennt man Betragsstriche und bedeuten, dass das Vorzeichen der Zahl weggelassen werden muss.
Das heißt:
½-5½=5
½5½=5
Formal ausgedrückt wird dies so:
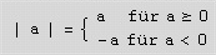
Andere Ausdrücke für |x|<2 sind:
-2 < x < 2 oder
-2 < x Ù x < 2
Aus dem letzten Ausdruck wird auch schon klar, wie man Betragsungleichungen lösen kann. Versuch es bei folgendem Beispiel:
|x+1|<5
Die Musterlösung findest du
hier!
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



