|
1.1 Vorbemerkung
|
|
SCHÜLERGLEICHUNG:
"großes neues Themengebiet" + "neue Rechentechniken" + "neue Grundidee" + "überhaupt alles neu" = AAAANGST!!!
ÄNDERUNGSVORSCHLAG:
"Schritt für Schritt herantasten" + "über neue Grundidee nachdenken" + "üben" = AHA-Erlebnis + Können
Was in diesem Lernpfad folgt kann also als Versuch
gesehen werden, der obigen Schülergleichung entgegenzuwirken,
sie im Idealfall sogar zu revidieren.
Zunächst stellt sich uns erstmal die Frage: Was ist denn dieses "Differenzieren" überhaupt? - Dieser Frage ist das vorliegende Kapitel gewidmet.
|
|
1.2 Die Grundidee - geometrisch
|
|
Also, prinzipiell hat das Differenzieren - oder auch Ableiten - etwas mit Funktionen zu tun: Man kann eine Funktion differenzieren/ableiten.
Außerdem hat das Differenzieren - ganz vage ausgedrückt - etwas mit Änderung zu tun, und zwar mit der Änderung in einem Punkt.
So weit so gut. Aber weitergebracht hat uns das noch nicht wirklich. Also überlegen wir zunächst einmal, wie wir das Differenzieren geometrisch deuten
können. Dadurch wird hoffentlich auch klarer, was dabei passiert.
Dass eine Funktion als Graph darstellbar ist, wissen wir ja schon. Stellen wir uns also eine beliebige Funktion als Graph vor. Nun interessiert uns, wie stark
dieser Graph in einem Punkt ansteigt. Das ist die zentrale Frage. Um sie zu beantworten, müssen wir die Funktion im gesuchten Punkt differenzieren/ableiten.
Differenzieren liefert uns also die Steigung eines Graphen in einem Punkt.
Jetzt müssen wir nur noch nachvollziehen, was die Steigung in einem Punkt überhaupt ist, und schon haben wir eine Vorstellung vom Differenzieren entwickelt.
Wir wollen dazu in 3 Denkschritten vorgehen:
Denkschritt 1: Steigung einer linearen Funktion (Steigungsdreieck)
Nehmen wir eine beliebige lineare (genauer: affine) Funktion, zB f(x) = 2x +1, und interpretieren sie wiederum als Graph:
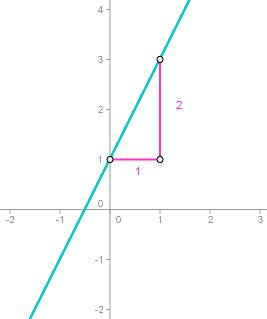
Wenn wir nun auf der x-Achse um 1 nach rechts wandern, steigt der Graph (und somit der Funktionswert f(x)) um 2. Die Funktion hat also die Steigung 2. Soweit kennen
wir das ja vom Steigungsdreieck. Da der Graph eine Gerade ist, wissen wir zudem, dass die Steigung überall gleich ist. Die Steigung ist in jedem Punkt dieselbe: 2.
Wichtig für uns ist nun, dass wir die Steigung auch als Verhältnis auffassen können, und zwar als Verhältnis der Änderung der x-Werte (Argumentwerte) zur Änderung
der y-Werte (Funktionswerte) auffassen kann. Wir wissen y (also f(x)) steigt um 2, wenn x um 1 zunimmt. Es gilt also das Verhältnis 2:1.
Sehen wir uns ein größeres Steigungsdreieck (mit Schrittlänge 2) an:
Hier steigt y (also f(x)) um 4, wenn x um 2 zunimmt. Es herrscht also das Verhältnis 4:2. Dieses Verhältnis lässt sich kürzen, wir erhalten 4:2 = 2:1. Also wieder
dasselbe Verhältnis 2:1. Was nicht wundert, schließlich handelt es sich um dieselbe lineare Funktion.
Um auf 4:2 zu kommen haben wir übrigens so gerechnet - und das ist der springende Punkt bei diesem Denkschritt! :
In Worten:
Differenz der y-Werte (Funktionswerte) dividiert durch Differenz der x-Werte (Argumentwerte), oder anders: Funktionswertänderung je Argumentwertänderung.
Denkschritt 2: Steigung einer nicht-linearen Funktion - Durchschnittliche Steigung (auf einem Funktionsabschnitt)
Nun nehmen wir eine beliebige nicht-lineare Funktion, zB f(x) = x² - 2.
Wieder interessiert uns die Steigung. Dummerweise ist die nun aber nicht mehr in jedem Punkt dieselbe.
im Punkt x = 0 ist die Steigung anders als im Punkt x = 0,1. Im Punkt x = 0,1 ist die Steigung anders als in x = 0.2 und so weiter. Also begnügen wir uns vorerst mit
der durchschnittlichen Steigung. Nehmen wir also an, wir bewegen uns auf der x-Achse um 1 nach rechts. Dann steigt y (f(x)) um 2. Das ist unsere durchschnittliche Steigung.
Kurz gesagt: Wir ignorieren, dass die Funktion nicht linear ist und rechnen genauso wie vorher:
Der einzige Unterschied zu vorher ist: Diesmal erhalten wir auf diese Art nur die durchschnittliche Steigung und nicht die Steigung in jedem Punkt. Ein Schritt fehlt uns also noch.
Denkschritt 3: Von der durchschnittlichen Steigung zur Steigung in einem Punkt
Vorhin haben wir die durchschnittliche Steigung der Funktion von x = 0 bis x = 1 berechnet - also im Intervall [0,1]. Genauer wäre die Sache schon, wenn wir das Intervall verkleinern und den
Durchschnitt von x = 0,5 bis x = 1 betrachten (Intervall [0.5, 1]. Je kleiner das Intervall, desto genauer der Durchschnittswert. Die folgenden Graphiken sollen das Prinzip verdeutlichen:
Du kannst dir die Sache auch in folgendem Link ansehen: vom_Durchschnitt_zum_Punkt.
Unser Ziel ist also: Intervall soweit verkleinern, dass die Intervall-Länge gegen Null geht. Dann sind wir bei der Steigung in einem Punkt angelangt.
Wie sieht das mit unserer Formel von vorhin aus?
Diese Formel lässt sich ja auch so schreiben:
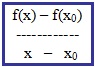
Wenn nun die Länge des Intervalls [a,b] bzw. [x,x0] gegen Null gehen soll, muss b - a = 0 sein. Also soll b = a sein.
Oder: x - x0 = 0, also x = x0. Jetzt sind wir am Ziel. Wir wollen x gegen x0 gehen lassen, müssen also den entsprechenden Grenzwert bilden:
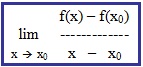
Dieser Grenzwert gibt uns nun die Steigung in einem Punkt an. Man bezeichnet ihn auch als die erste Ableitung.
Und jetzt die gut Nachricht: Wir müssen nicht jedesmal eine Grenzwertberechnung durchführen, wenn wir uns für die Ableitung interessieren:
Es gibt eine Reihe von Rechenregeln beim Differenzieren, mit denen wir uns die Grenzwertberechnung quasi ersparen. Diese lernen wir im nächsten Kapitel kennen.
Vorab aber noch etwas zum Grenzwert. Es gibt eine wesentlich kürzere Schreibweise für ihn - man bezeichnet die erste Ableitung auch mit f '(x).
In einem Steigungdreieck wäre der Grenzwert/die erste Ableitung/f '(x) übrigens gleichbedeutend mit der Steigung (dem Wert bei der senkrechten Dreiecksseite):
Auch zu diesem Sachverhalt gibt es einen nützlichen Link: Steigung_in_einem_Punkt.
Arbeitsauftrag:
1) Lies dir den Abschnitt 1.2 durch und schreibe in deinen eigenen Worten eine Zusammenfassung.
2) Sieh dir im Schulbuch oder im Internet Einträge zu den Themen "Differenzenquotient" und "Differenzialquotient" an. Was haben diese Begriffe mit Abschnitt 1.2 zu tun?
(Eintrag ins Arbeitsheft)
Lernstoff, Arbeitsheft-Eintrag
|
|
1.3 Vorläufige Zusammenfassung
|
|
- Differenzieren ist etwas, dass man mit einer Funktion machen kann.
- Differenzieren liefert uns die Steigung eines Graphen in einem Punkt.
- Bei einer linearen Funktion sieht man die Steigung am Steigungsdreieck oder berechnet sie mit folgender Formel:
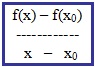
- Bei einer nicht-linearen Funktion liefert obige Formel die durchschnittliche Steigung.
- Die Steigung in einem Punkt erhält man, indem man bei obiger Formel das Intervall [x,x0] gegen Null gehen lässt, und zwar durch Bilden des Grenzwertes:
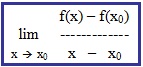
- Dieser Grenzwert wird auch erste Ableitung genannt und mit f '(x) bezeichnet.
- Im Steigungsdreieck entspricht f '(x) wiederum genau der Steigung.
Zusammenfassung
|
|
1.4 Wichtige Ergänzung - Differenzierbarkeit
|
|
Man kann übrigens nicht jede Funktion ableiten! Damit eine Funktion in einem Punkt differenzierbar ist, muss in diesem Punkt der Grenzwert:
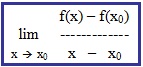existieren.
(Das ist der Fall, wenn der entsprechende rechtsseitige und der entsprechende linksseitige Grenzwert existieren und diese gleich sind.)
Ist eine Funktion in allen Punkten des Definitionsbereiches differenzierbar, spricht man von einer differenzierbaren Funktion.
Die folgenden Abschnitte beziehen sich ausschließlich auf differenzierbare Funktionen.
Arbeitsauftrag:
Versuche eine Funktion zu finden, die nicht differenzierbar ist! (Eintrag ins Arbeitsheft)
Lernstoff, Arbeitsheft-Eintrag
|
|
1.5 Historische Bemerkungen
|
|
Die Differenzialrechnung wurde Ende des 17. Jahrhunderts entwickelt. Die heute übliche Schreibweise existiert seit Ende des 19. Jahrhunderts. Schulstoff wurde das
Differenzieren 1905, da die fortschreitende Entwicklung von Technik und Wirtschaft einen verstärkten Einsatz der Differenzialrechnung mit sich brachte.
Gehen wir aber nochmal kurz zurück ins 17. Jahrhundert. Wer hatte die zündende Idee?
Leibniz und das Tangentenproblem
Gottfried Wilhelm Leibniz hat die Differenzialrechnung entwickelt, indem er das Tangentenproblem löste: Welche Geradce beschreibt die Steigung einer Funktion in
einem Punkt am besten? (Dieser Ansatz ist für uns ja nun nichts Neues mehr.)
Dabei entspräche die Steigung einer Sekante (also einer Geraden, die den Funktionsgraphen im betrachteten Abschnitt zweimal schneidet) unserer Formel für die
durchschnittliche Steigung:
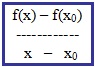
Die Steigung der Tangente entspricht genau unserer Formel für die Steigung in einem Punkt:
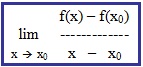
Newton und die Momentangeschwindigkeit
(Ja, sapperlot  - da hat doch tatsächlich noch ein zweiter Mathematiker dasselbe entwickelt!
Zur selben Zeit, Ende des 17. Jahrhunderts, hat auch Isaac Newton - unabhängig von Leibniz - die Differenzialrechnung entwickelt. Sein Ausgangsproblem war jedoch
ein anderes: Newton beschäftigte sich mit der Momentangeschwindigkeit.
Wenn wir die durchschnittliche Geschwindigkeit als zurückgelegten Weg pro Zeitintervall betrachten (Geschwindigkeit misst man ja auch in Metern pro Sekunde),
können wir die durchschnittliche Geschwindigkeit mit folgender Formel berechnen:
(Hierbei ist t die Zeit, s(t) der Weg in Abhängigkeit der Zeit.)
Die Geschwindigkeit zu einem Zeitpunkt - die Momentangeschwindigkeit - erhält man dann, indem man das gewählte Zeitintervall gegen Null gehen lässt. Die Formel zur
Berechnung der Momentangeschwindigkeit sieht somit wie folgt aus:
Und damit sind wir wieder bei der ersten Ableitung gelandet.
Vertiefung
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|
