|
5.3 Physik und Technik
|

 

|
Geschwindigkeit und Beschleunigung
Geschwindigkeit und Beschleunigung lassen sich bequem als Ableitungen der Ortsfunktion berechnen.
Eng verwandt damit ist auch die Newtonsche Bewegungsgleichung (wiederum ein Abstecher in die Differenzialgleichungen).
(Siehe die auch diesen Link an.)

(Graphik: http://fotowettbewerb.hispeed.ch/seo/photo/19344/beschleunigung/yamaha_r1_beschleunigung_wheelie_motorrad_rennen.html)
Radioaktiver Zerfall
Wie lange dauert es, bis die Umgebung nach einem Kernkraftunfall wieder frei von radioaktivem Material ist?
Auch darauf hat die Mathematik eine Antwort: Radioaktiver_Zerfall (nutzt ebenfalls Differenzialgleichungen).

(Graphik: http://www.mpg.de/bilderBerichteDokumente/dokumentation/pressemitteilungen/2006/pressemitteilung200512221/index.html)
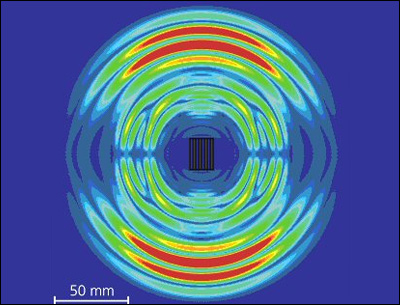
Schallwellen
Was für eine Geräusch macht eine Hand beim Klatschen? Nun, darauf hat auch die Mathematik keine Antwort.
Wie lange es hingegen dauern würde, bis ein 10 Meter entfernt stehender Mensch dies hört, ist wiederum
berechenbar. Sie dir dazu auch folgenden Link an: Schallwellen.
(Ja, richtig geraten, wieder ein Fall für die Differenzialgleichung.)
(Graphik: http://www.kompetenzcluster.org/leuchttuerme/news-anzeige/article/1363/6/neste/1/)
Wärmeleitung
Warum fühlt sich eine Badfliese kälter an als ein Holzboden, obwohl beide die gleiche (gemessene)
Temperatur haben? Wärmeleitung! Wer hat's berechnet? Ricol... Nein, doch die Mathematik.
Zur Differentialgleichung führt dich auch der folgende Link: Waermeleitungsgleichung.

(Graphik: http://www.karotten-express.de/energieberater/thermo.htm)
Airbag-Sensoren
Mathematik rettet Leben! Wer hätte das gedacht? (Nimm das, Schüler Gerber!)
Tatsächlich kann man mit Hilfe von Differentialgleichungen die Oberfläche
von Objekten beschreiben - was man zB bei Airbag-Sensoren sinnvoll nutzen
kann. Die folgenden Links liefern mehr Information zum Sachverhalt:
Entfaltung_von_Airbags
Level-Set-Methode_verbal
Level-Set-Methode_mathematisch

(Graphik: http://www.itwm.fhg.de/de/tv__tvprojects/airbag/)
(Es will an dieser Stelle nochmal kurz erwähnt werden, dass Differenzieren und Differenzialgleichungen
natürlich streng genommen zwei Paar Schuhe sind. Sie hängen jedoch zumindest soweit zusammen, dass
man Anwendungen von Differenzialgleichungen auch ohne schlechtes Gewissen im Zusammenhang mit dem
Differenzieren erwähnen kann.)
Praxisbezug
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



