|
3.1 Kettenregel
|

  
|
Betrachten wir nun verkettete Funktionen. Diese haben die Form f(g(x)). Sie bestehen also aus einer äußeren und einer inneren Funktion.
Ein Beispiel: (3x - 10)5: äußere Funktion ( )5; innere Funktion 3x - 10.
Ein weiteres Beispiel: sin(5x): äußere Funktion sin( ); innere Funktion 5x.
TIPP: Stell dir statt der Variablen (üblicherweise x) Zahlen vor - dann gilt folgende Faustregel:
Die zuerst zu befolgende Rechenoperation ist die der inneren Funktion,
die zuletzt zu befolgende Rechenoperation ist die der äußeren Funktion.
Für solche verketteten Funktionen gilt nun folgende Regel:
Ableitung der äußeren Funktion mal Ableitung der inneren Funktion. Als Formel:
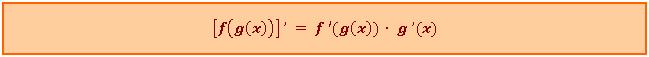
bzw:

Eine dritte Schreibweise verwendet folgende Symbole:

(Dabei bedeutet df/dx (sprich: "df nach dx") Ableitung von f(x) nach x, also f '(x).)
Arbeitsauftrag:
1) Wähle die Schreibweise, die dir am einfachsten erscheint, und notiere sie in deinem Arbeitsheft. Füge auch eine Erklärung in eigenen Worten und ein Beispiel hinzu.
2) Löse folgende Hotpotatoes-Datei: Advanced_Kettenregel.
Mache einen Screenshot der gelösten Aufgabe und klebe ihn in dein Arbeitsheft.
3) Die Regel für 2 verkettete Funktionen kennst du nun schon. Wie aber sieht die Regel für mehrere verkettete Funktionen aus?
Kannst du Regel (in der Schreibweise deiner Wahl) auf 3 verkettete Funktionen erweitern? (Eintrag ins Arbeitsheft)
Lernstoff, Arbeitsheft-Eintrag
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



