|
1.1 Normalaufstellung
|

 

|
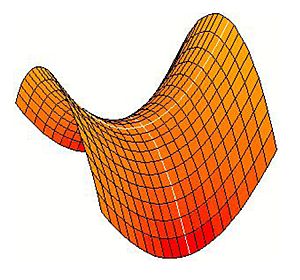
Das Hyperbolische Paraboloid, kurz HP, ist in der Grund-/ Normalaufstellung durch die Gleichung
x²/a² - y²/b² + z = 0
gegeben. Es ist eine Fläche 2. Ordnung und wird aufgrund der Form auch als Sattelfläche bezeichnet.
Das HP kann auf zwei Arten erzeugt werden:
Lernstoff
|
|
1.2 Das HP als Schiebfläche
|

 

|
Gegeben seien zwei Parabeln mit folgenden Eigenschaften:
- die Ebenen der Parabeln sind zueinander normal
- die Achsen der Parabeln stimmen überein
- die Scheitel der Parabeln stimmen überein
- die Parabeln sind nach verschiedenen Seiten hin geöffnet
Wird nun eine der beiden Parabeln so verschoben, dass ihr Scheitel die andere Parabel durchläuft, entsteht ein HP.

Lernstoff
|
|
1.4 Animation
|

 

|
Hier
kannst du ein HP von allen Seiten betrachten.
Auf dieser
Seite
findest du ein Video zum HP als Regelfläche.
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



