|
4.1 Schnitte mit lotrechten Ebenen
|

 

|
Ebenen parallel zur Auf- und Kreuzrissebene:
Aufgrund der Art der Enstehung des HP als Schiebfläche ergeben sich als
Schnittkurven jeweils Parabeln.
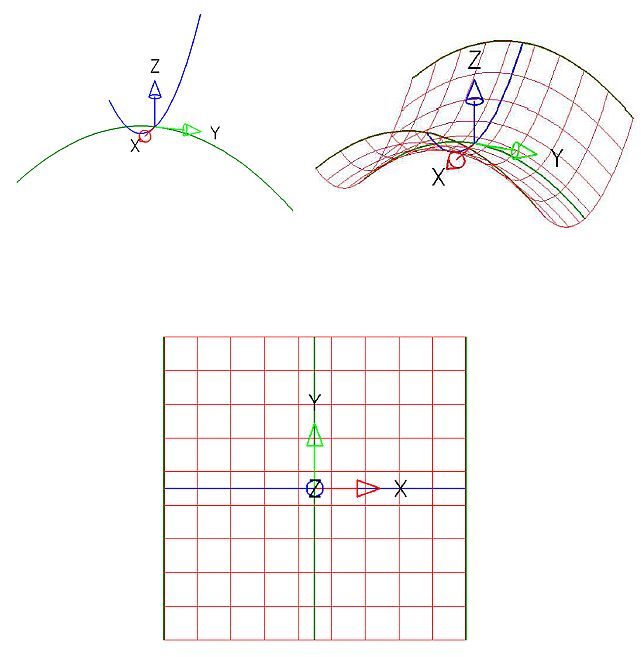
Alle anderen lotrechten Ebenen, die nicht zur Auf- und Kreuzrissebene parallel sind,
schneiden das HP entweder ebenfalls jeweils nach einer Parabel oder nach einer Gerade
(dabei handelt es sich um eine e- oder f-Erzeugende, die betreffende Schnittebene ist in diesem Fall eine Richtebene).
Lernstoff
|
|
4.2 Ebenen parallel zur Grundrissebene
|

 

|
Betrachtet man die Ebene z = k, dann findet man für die Schnittkurve die Darstellung:
y2/b2 - x2/a2 = k
Dies ist i.a. eine Hyperbel.

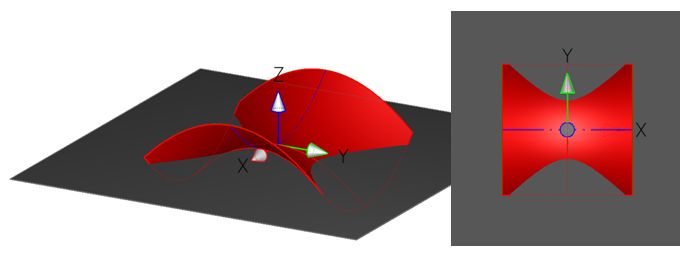
Für k = 0, also für die Grundrissebene, ergibt sich:
x/a + y/b = 0 und x/a - y/b = 0
Dh. die Schnittkurve zerfällt in zwei Geraden(eine e- und eine f-Erzeugende).
Diese beiden Geraden werden als Scheitelerzeugende des hyperbolischen
Paraboloides bezeichnet. Ihr Schnittpunkt liegt auf der Achse der hyperbolischen
Paraboloides und heißt Scheitel.

Lernstoff
|
|
4.3 Allgemeine Ebenen
|

 

|
Alle anderen Ebenen schneiden das HP jeweils entweder nach einer Hyperbel oder
nach zwei Geraden (nach einer e- und einer f-Erzeugenden).
Lernstoff
|
|
4.5 Selbsttest
|

 

|
Teste deinen bisherigen Wissensstand mittels eines
Multiple-Choice Tests
zum Thema Ebene Schnitte des HPs
oder eines
Kreuzworträtsels,
das sich mit den ebenen Schnitten des HPs und seiner Symmetrie befasst.
Selfchecking Test
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



