|
4.1 Informationen und Eigenschaften
|

 

|
Lies dir dieses Unterkapitel gut durch!
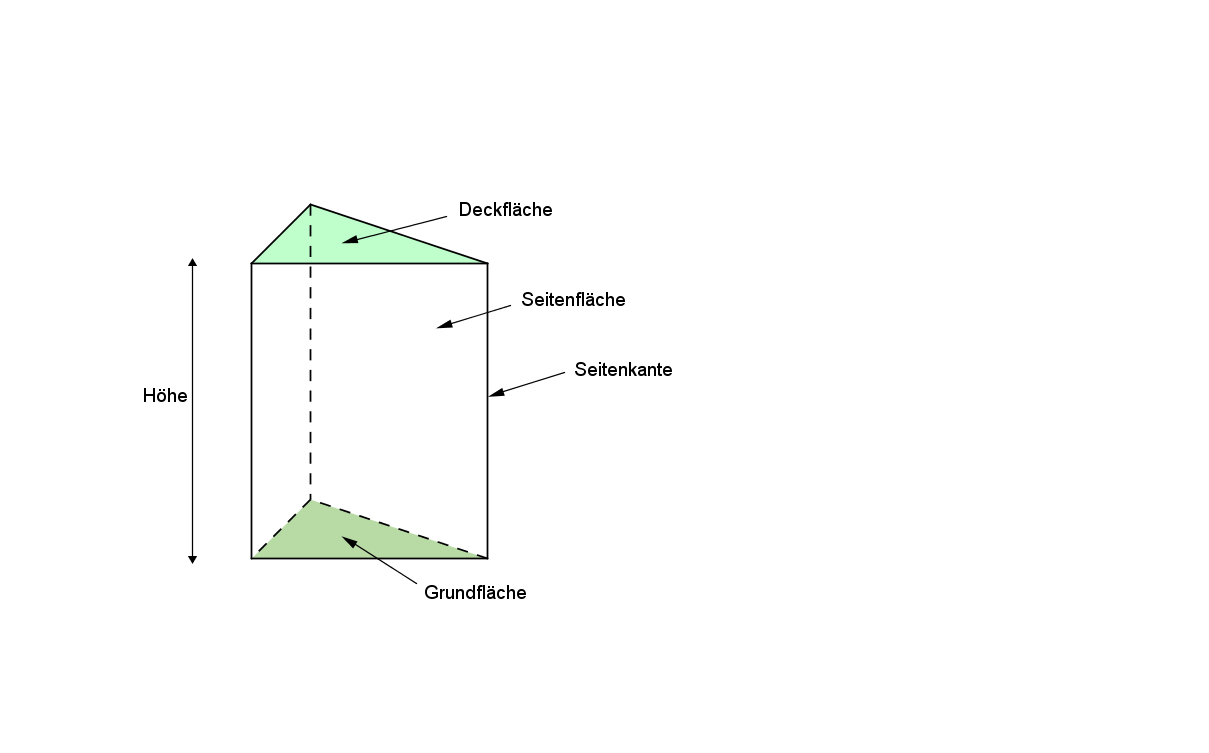
Ein gerades Prisma wir von zwei zueinander parallelen und deckungsgleichen (kongruenten) Vielecken sowie von Rechtecken begrenzt.
Die beiden zueinander parallelen und deckungsgleichen Vielecke heißen Grundflächen, die Rechtecke heißen Seitenflächen.
Die Seitenflächen bilden zusammen die Mantelfläche des Prismas..
Alle Seitenkanten sind zueinander parallel und gleich lang. Beim geraden Prisma stehen die Seitenkanten normal zur Grundfläche.
Ist die Grundfläche ein Dreieck (Viereck, Fünfeck, ...), so heißt das Prisma dreiseitiges (vierseitiges, fünfseitiges, ...) Prisma.
Ein Prisma wird also nach seiner Grundfläche (Querschnittsfläche) benannt.
Der Abstand zwischen Grund- und Deckfläche des Prismas wird Höhe des Prisma genannt.
Das gleichseitige Dreieck, das Quadrat und die regelmäßigen Vielecke bezeichnet man als regelmäßige Figuren.
Ein gerades Prisma mit einer regelmäßigen Figur als Grundfläche wird daher als regelmäßiges Prisma bezeichnet.
Ein Quader ist ein besonderes Prisma.
Lernstoff
|
|
4.2 Oberfläche von Prismen
|

  

|
Übertrage dieses Unterkapitel in dein Schulübungsheft bzw. Lerntagebuch!
Breitet man die Begrenzungsflächen eines Prismas in der Ebene aus, so erhält man das Netz des Prismas.
Die Oberfläche O eines geraden Prismas besteht aus der Grundlfäche G, der gleich großen Deckfläche und der Mantelfläche M.
O = 2 · G + M
Der ausgebreitete Mantel eines geraden Prismas ist ein Rechteck mit den Seitenlänge uG und h.
uG ist der Umfang der Grundfläche G und h ist die Höhe des Prismas.
M = uG · h

Lernstoff, Eintrag in das Lerntagebuch
|
|
4.3 Volumen von Prismen
|

  

|
Übertrage dieses Unterkapitel in dein Schulübungsheft bzw. Lerntagebuch!
Das Volumen eines Prismas mit der Grundfläche G und der Körperhöhe h kann mithilfe
folgender Formel berechnet werden:
V = G · h
Beispiel:
Prisma mit rechtwinkligem Dreieck als Grundfläche: V = G · h = ½ · a · b · h
Lernstoff, Eintrag in das Lerntagebuch
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



