2.1 Vektoraddition
http://http://www.mathe-online.at/lernpfade/vektoren/tutor/?kapitel=2
|

 
|
Zwei Vektoren werden addiert, indem man ihre Koordinaten komponentenweise addiert.
Graphisch werden zwei Vektoren addiert, indem man den Anfangspunkt des ersten Vektors mit dem Endpunkt des zweiten Vektors verbindet, wobei die Spitze des ersten Vektors der Anfangspunkt des zweiten ist.
graphische Veranschaulichung:
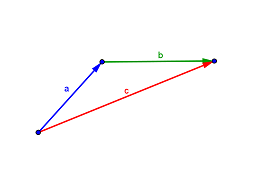
Der Vektor b addiert zum Vektor a ergibt den Vektor c.
Den nun erhaltenen Vektor c bezeichnet man auch als Summenvektor.
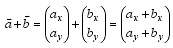
Teste dich selbst !
|
2.5 skalares Produkt
http://http://www.mathe-online.at/lernpfade/vektoren/tutor/?kapitel=2
|

 

|
Nach dem Kapitel 2.3 wissen wir nun was mit dem Vektor passiert, wenn er mit einem Skalar multipliziert wird.
Nun stellen wir uns aber noch die Frage, wie zwei Vektoren multipliziert werden?
Die Antwort stellt sich nicht als besonders schwierig oder kompliziert heraus.
Das Skalarprodukt, auch genannt inneres Produkt, errechnet sich folgendermaßen:
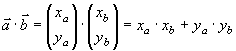
Orthogonalitätsbedingung:
Das skalare Produkt ist genau dann Null, wenn einer der Vektoren der Nullvektor
ist, oder wenn die Länge der Projektion des einen Vektors auf den anderen gleich Null ist. Das
ist nur dann der Fall, wenn die beiden Vektoren aufeinander normal stehen, d.h. wenn der
Winkel, den die Vektoren einschließen, gleich 90° ist.
|
2.6 Einheitsvektor
http://http://www.mathe-online.at/lernpfade/vektoren/tutor/?kapitel=2
|

 

|
Ein Vektor mit der Länge 1 heißt Einheitsvektor.
Um den Einheitsvektor eines Vektors berechnen zu können,ist es wichtig die Länge des Vektors zu kennen und seine Komponenten.
Zur Berechnung des Einheitsvektors werden die einzelnen Komponenten (x,y) durch den Betrag (=Länge) des Vektors dividiert.
Dieser Vorgang wird "Nominieren eines Vektors" genannt.
Einheitsvektoren erfüllen zwei besondere Aufgaben:
- Die Richtung des Vektors kann unabhängig von der Länge angegeben werden.
- Zum Abtragen vorgegebener Lägen kann der Einheitsvektor mehrmals abgetragen werden.
Beispiel:
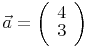
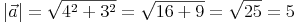

|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



