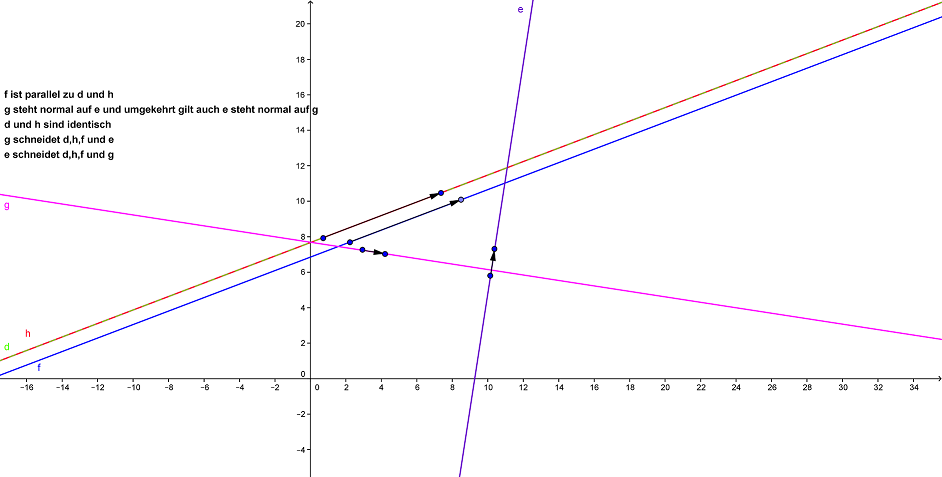
Fall 1:
![](http://www.mathe-online.at/materialien/nadine.hampel/files/Vektoren_im_R2/schneidend1.png")
Die Geraden haben einen Schnittpunkt, sie sind also schneidend.
Fall 2:
![](http://www.mathe-online.at/materialien/nadine.hampel/files/Vektoren_im_R2/parallel1.png")
Die Geraden haben keinen Schnittpunkt, sie sind also parallel.
Fall 3:
![](http://www.mathe-online.at/materialien/nadine.hampel/files/Vektoren_im_R2/identisch1.png")
Die Geraden haben unendlich viele Schnittpunkte, sie sind also identisch.
Ein Gleichungssystem aus zwei linearen Gleichungen hat bekanntlich entweder eine, keine oder unendlich viele Lösungen.
Was aber hat das mit der Lage zweier Geraden zu tun?
Wenn wir zwei Geraden schneiden machen wir praktisch nichts anderes als ein Gleichungssystem aus zwei Gleichungen mit zwei Unbekannten (x,y) zu lösen.
Hat dieses Gleichungssystem genau eine Lösung, schneiden sich die beiden Geraden in genau einem Punkt.
Hat das Gleichungssystem unendlich viele Lösungen, sind die Geraden identisch und erhält man gar keine Lösung sind die Geraden parallel, da sie sich in keinem Punkt schneiden.
Hier ein kleiner Überblick !
|
