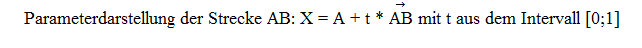
Jedem Punkt X der Strecke ist genau ein Parameterwert t aus dem Intervall [0;1] zugeordnet. Durchläuft t alle Zahlen des Intervalls [0;1], so durchläuft X alle Punkte der Strecke AB. Mit anderen Worten:
Die Parameterdarstellung stellt eine eindeutige Zuordnung zwischen den Zahlen des Intervalls [0;1] und den Punkten der Strecke AB her.

Jedem Punkt der Geraden g ist genau ein Parameterwert t aus den reellen Zahlen zugeordnet.
D.h: Die Parameterdarstellung beschreibt eine eindeutige Zuordnung zwischen den Punkten der Geraden und den reellen Zahlen. Durchläuft t alle reellen Zahlen, so durchläuft X alle Punkte der Geraden, und umgekehrt.
|



