Falls Sie Probleme haben das Applet auszuführen, lesen Sie bitte hier, welche Voraussetzungen ihr Browser haben muss, um unsere Applets anzeigen zu können.
Für den theoretischen Hintergrund des Applets verweisen wir auf den Artikel Dynamische Systeme (3D).
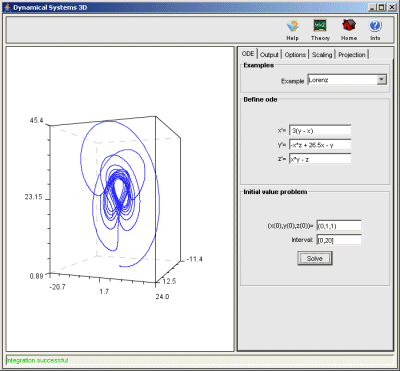
The easiest way to see how you can use the applet in order to draw orbits
of a 3d ordinary differential equation is to load one of the predefined
examples, accessible via the combo-box Examples.
Otherwise you have to enter the components of the ode in the fields
x', y' and
z' (read here about the
syntax to use).
After entering an initial value and an integration interval in the fields
As already mentioned, you can find information on details of the integration under the tab Output. By clicking the right mouse button a pop-up window is shown, where you can clear the output. Further you can choose whether the output of the last computation should be displayed only.
Under the tab Options you can set the options for the ode solver. (We use a 5th order embedded explicit Runge-Kutta integrator with adaptive step size control.) Under the options General Options you can enter the maximum number of steps the ode solver is allowed to execute. Moreover, you can enable or disable the dense output of the solver, which ensures that the plotted curve looks smooth, even if the solver uses a few steps only. Under the options Step size options the (initial) step size can be altered. If the option Step size control is disabled this step size will be used for the whole integration. If Step size control is enabled the intial step size is adaptively changed. If this option is enabled the desired accuracy for the integration must be entered in the field Local error.

Under the tab Scaling you can change the scaling of the axes. Moreover, you can choose there if a bounding box and labels should be displayed.
Under the tab Projection you can
switch between perspective and parallel projection. In case of
the perspective projection you can adjust the distance between
the center of projection and the plane of projection. In the case of parallel
projection you can
choose between different planes of projection.