Mathematische Symbole
und Abkürzungen

Die folgende Tabelle listet die wichtigsten Symbole und Abkürzungen auf, die in mathe online eine Rolle spielen. In der zweiten Spalte ist die Bedeutung des jeweiligen Symbols angegeben. Falls das Symbol in den Mathematischen Hintergründen definiert oder beschrieben wird, ist diese Eintragung ein Link, der Sie an die entsprechende Stelle führt. Die dritte Spalte ist Bemerkungen und Beispielen vorbehalten.
Þ daraus folgt   Beispiel:  n ist durch 4 teilbar  Þ  n ist durch 2 teilbar
Û genau dann, wenn   Beispiel:  n ist eine gerade Zahl  Û  n ist durch 2 teilbar
» ungefähr gleich   Beispiel: 1/3 »  0.33
¹ ungleich   Beispiel: 2 ¹ 1
< kleiner   Beispiel: 1 < 2
> größer   Beispiel: 2 > 1
£ kleiner-gleich   Beispiel: -x2 £ 0 für jede reelle Zahl x
³ größer-gleich   Beispiel: x2 ³ 0 für jede reelle Zahl x
º identisch   Beispiel: a × a º a2
± plus-minus   Beispiel: Aus x2  = 4  folgt  x = ± 2  (d.h. x = -2 oder x = 2)
{ ¼} Menge   Beispiel:  A = {1, 4, 9, 16, 25}
N oder $\mathbb{N}$ Menge der natürlichen Zahlen   N = {1, 2, 3, ¼}
  Achtung: Manchmal wird die Null zur Menge N hinzugenommen.
Z oder $\mathbb{Z}$ Menge der ganzen Zahlen   Z = {¼, -3, -2, -1, 0, 1, 2, 3, ¼}
Q oder $\mathbb{Q}$ Menge der rationalen Zahlen   Menge aller Bruchzahlen  m/n  (wobei m, n ganzzahlig und n ¹ 0)
R oder $\mathbb{R}$ Menge der reellen Zahlen   Menge aller Zahlen mit Dezimaldarstellung
C oder $\mathbb{C}$ Menge der komplexen Zahlen   Menge aller $x+iy$ mit $x,y\in\mathbb{R}$
(a, b) offenes Intervall   Achtung: Verwechslungsgefahr mit "geordnetes Paar" (s.u.)
[a, b] abgeschlossenes Intervall   [a, b) und (a, b] bezeichnen halboffene Intervalle.
¥ unendlich  
| ¼ | Absolutbetrag   Beispiele:  | 5 | = 5, | -6 | = 6
   _
Ö
 (Quadrat-)Wurzel   Wird der Einfachheit halber oft auch als  Ö  geschrieben.
  Für (nicht-negative) reelle Zahlen ist sie immer ³ 0 (z.B. Ö4 = 2).
p Kreiszahl (Pi)   p = 3.1415926535897932384626433832795... »  3.14 
Î ist Element von   Beispiel:  5 Î N
Ï ist kein Element von   Beispiel:  ½  Ï N
" für alle (für jedes)   Beispiel:  x y = y x   " x, y Î R
$ es existiert ein   Beispiel:  $ a Î R, sodaß gilt:  a2 = 2
| für die gilt   { x | ¼} = Menge aller x, für die gilt ¼
Ç Durchschnittsmenge   A Ç B = { x | x Î A und x Î B }
È Vereinigungsmenge   A È B = { x | x Î A oder x Î B }
Í ist Teilmenge von   Beispiel:  N Í Z
Ê    ist Obermenge von      Beispiel:  Z Ê N
\ Komplementärmenge   A \ B = { x Î A | x Ï B }
  Dafür sind auch die Schreibweisen  A ~ B  und  A – B  gebräuchlich.
^ hochstellen (Potenz)   Beispiel: Schreibweise x^2 anstelle von x2
Ù logisches und  
Ú logisches oder  
Ø logisches nicht  
{ } leere Menge   Dafür ist auch das Symbol  f  gebräuchlich.
@ isomorph   Kann im konkreten Fall verschiedene Bedeutungen haben,
  z.B., daß zwei Mengen "gleichmächtig" sind.
(a, b) geordnetes Paar   Achtung: Verwechslungsgefahr mit "offenes Intervall" (s.o.)
× kartesisches Produkt
zweier Mengen		   A × B = { (a, b) | a Î A, b Î B }. Ausgesprochen: "A kreuz B ".
  Manchmal auch für die Multiplikation zweier Zahlen verwendet.
R2 zweidimensionaler Raum   Mathematische Formalisierung der Zeichenebene als R × R .
  Ausgesprochen:  "R zwei".
R3 dreidimensionaler Raum   Formalisierung des dreidimensionalen Raumes als R × R × R .
  Verallgemeinerung: Rn (n = 4, 5, ¼).
a Vektor   Vektoren werden fett daregstellt.
  Beispiel: a = (3, 4).
| ¼ | Betrag eines Vektors   Beispiel: | (3, 4) | = 5.
|| parallel   Schreibweise: a || b
^ normal (orthogonal)   Schreibweise: a ^ b
D Dreieck   Schreibweise für das Dreieck mit Eckpunkten A, B und C: DABC
  Achtung: Verwechslungsgefahr mit "Änderung" (s.u.)
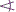Winkelsymbol Winkel   Schreibweise: 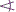WinkelsymbolCAB (für den Winkel mit Scheitel A).
f(x) Zuordnungsvorschrift für
Funktionen		   Beispiel: Durch  f(x) = x3  ist eine Funktion  f : R ® R  definiert.
o Verkettung von Funktionen   (f o g) (x)  =  f (g(x))
® Zuordnungsvorschrift für
Funktionen		   Beispiel: Durch  f : x ® x2  ist eine Funktion  f : R ® R  definiert.
® asymptotisches Verhalten:
"gegen"		   Beispiel: x2 wächst für x ® ¥ ("x gegen Unendlich") über jede Schranke.
e Eulersche Zahl   e = 2.7182818284590452353602874713526... »  2.718 
| bedingte Wahrscheinlichkeit   Schreibweise: p(A|B)
< ...> Erwartungswert   Beispiel: < a > für den Erwartungswert der Zufallsvariable a.
  Eine andere Schreibweise dafür ist E(a).
m Erwartungswert   Übliche Bezeichnung für den Erwartungswert einer Zufallsvariable.
s2 Varianz   Übliche Bezeichnung für die Varianz einer Zufallsvariable.
s Standardabweichung   Übliche Bezeichnung für die Standardabweichung einer Zufallsvariable.
' Ableitung   Beispiel: (x2) ' = 20x
'' Zweite Ableitung   Beispiel: (x3) '0' = 60x
D Differenz, Änderung   Differenzenquotient: Df/Dx
  Achtung: Verwechslungsgefahr mit "Dreieck" (s.o.)
d Differential   Ableitung ("Differentialquotient"): df/dx.
  Dies wird ausgesprochen als "df nach dx".
d/dx Differenzieren   Beispiel: d(x2)/dx = 20x.
  Ausgesprochen: "d nach dx von ...".
d2/dx2 Zweimal differenzieren   Beispiel: d2(sin x)/dx2  =  -0sin x.
  Ausgesprochen: "d zwei nach dx-Quadrat von ...".
| an der Stelle   Beispiel: (x2) ' |x=5  =  10
ò ... dx unbestimmtes Integral   Beispiel: ò x2 dx  =  x3/3
òab ... dx bestimmtes Integral   Beispiel: ò03 x2 dx  =  9
| Differenz an den Stellen   Wird für das bestimmte Integral verwendet.
  Beispiel: ò12 3x2 dx  =  x3 |12  =  23 - 13  =  7 

 Zur Galerie
 Zu den Mathematischen Hintergründen
 Zum Lexikon
 Zu den interaktiven Tests
 Zu den Mathe-Links und Online-Werkzeugen
 Zur Welcome Page 		   Übersicht über die Lernpfade
 Open Studio Materialien
 Open Studio Eingang