1.1 Begriffserklärung, Definition
|

 

|
Als Einstieg in das Thema Potenzen sehen wir uns erst einmal die Definition an:
Defintion 1.1.1: Ist aÎR und nÎN, dann schreibt man:
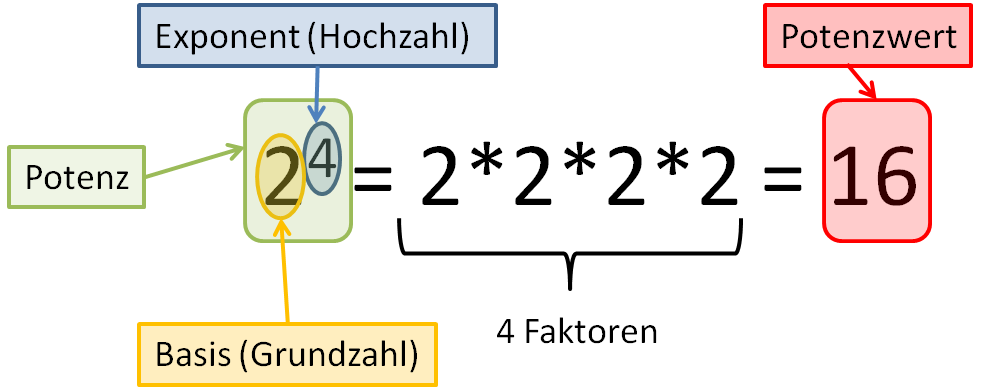
an = a·a·a·...·a (für n³2 und n Faktoren a)
Ferner setzt man: a1 = a
Man bezeichnet a als Basis (oder Grundzahl), n als Exponent (oder Hochzahl) und an als Potenz
Lernstoff
|
1.2 Sätze und Rechenregeln
|

  
|
Nun, da wir die grundlegenden Begriffe eingeführt haben, wenden wir uns den wichtigen Rechenregeln zu. Beachte, dass dieser Abschnitt dich mit Regeln vertraut macht, die du auch später noch oft brauchen wirst!
Satz 1.2.1: Für alle a, bÎR und für alle n, mÎN gilt:
(1) am·an=am+n
(2) am/ an= am-n für a¹0 und m >n
am/ an=1/ an-m für a¹0 und m <n
(3) (am)n=am ·n
(4) (a ·b)n=an ·bn
(5) (a/b)n= an/ bn für b¹0
Wichtig: Dieser Satz beinhaltet alle Rechenregeln, die du zum Rechnen der Übungsbeispiele in diesem Kapitel brauchst. Falls du in der Stunde gefehlt hast, übertrage sie bitte in dein Schulübungsheft.
Satz 1.2.2: Ist aÎR und nÎN, dann gilt:
(1) (-a)n=an, falls n gerade
(2) (-a)n=-an, falls n ungerade
Dieser Satz sagt viel über den Grafen einer Potenzfunktion (Kapitel 3) aus.
Lernstoff
|
1.4 Anwendungen
|

 

|
Ihr habt schon gehört, dass Ausdrücke der Form an eine Vereinfachung der Schreibweise von Produkten mit gleichen Faktoren sind.
Diese Vereinfachung ist deshalb sinnvoll, weil es viele Anwendungen in der Praxis gibt, bei denen eben solche Produkte mit gleichen Potenzen vorkommen.
Hier ein paar davon:
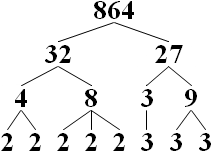
· Primpotenzen, Primfaktorzerlegungen (Wichtig in der Kryptographie, das heißt in der Datenverschlüsselung, insbesondere am PC)
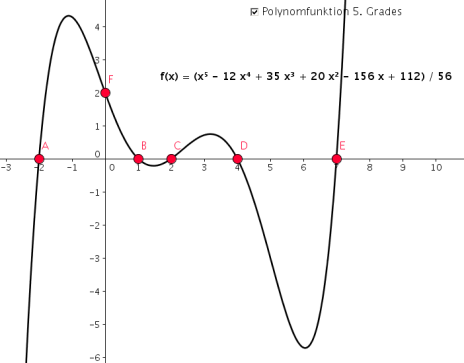
· Polynome (Polynome sind bei vielen mathematischen Anwendungen sehr wichtig, zum Beispiel bei Näherungsfunktionen. Wir werden ein eigenens Kapitel über sie durchmachen.)
· Zinsrechnung

Diese Anwendungen werde ich in der Stunde näher erläutern.
Zusätzlich zu diesen Anwendungen findest du Potenzen auch in der Geometrie (Flächen und Volumsberechnung), Physik (z.B. Beschleunigung), etc.
Praxisorientierung
|
1.5 Übungsbeispiele zum sofort machen
|

 

|
Hier kannst du überprüfen, ob du das Kapitel schon gut beherrschst.
Übung 1
Übung 2
Selfchecking Test
|
1.6 Beispiele für das Schulübungsheft
|

  
|
Beispiel 1.) Vereinfache so weit wie möglich: an/am+1·an-m
Beispiel 2.) Vereinfache so weit wie möglich: (½a)3·(2a3)4
Beispiel 3.) Berechne das Volumen eines Kegels mit r=4·103mm und h=3·103. (Hinweis: VK=(r2Õh)/3)
Beispiel 4.) Vereinfache so weit wie möglich: (ar/bs)3:(ar+1/bs+1)4
Übungsaufgaben
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



