3.1 Motivation und Begriffsdefinition
|

 

|
In folgendem Kapitel untersuchen wir durch Betrachten entsprechender Funktionen, wie sich Potenzen ändern, wenn sich der Exponent ändern. Dabei soll auch das Wissen über reele Funktionen erweitert werden.
Wiederholung:
(1) Was ist eine reele Funktion?
(2) Was ist der Graf einer reelen Funktion?
(3) Wann ist eine Funktion streng monoton steigend und wann streng monoton fallend?
Definition 3.1.1: Eine reele Funtion des Typs x®c·xn mit nÎN und cÎR heißt eine Potenzfunktion vom Grad n.
Beispiele: Die kinetische Energie aus der Physik E=½·m·v2 ist eine Potenzfunktion vom Grad 2. Das Kugelvolumen V=4·r3·Õ/3 ist eine Potenzfunktion vom Grad 3.
Wiederholung
|
3.2 Beispiele von Funktionsgrafen
|

  
|
Betrachten wir zuerst einmal die Potenzfunktionen mit geraden, natürlichen Exponenten:
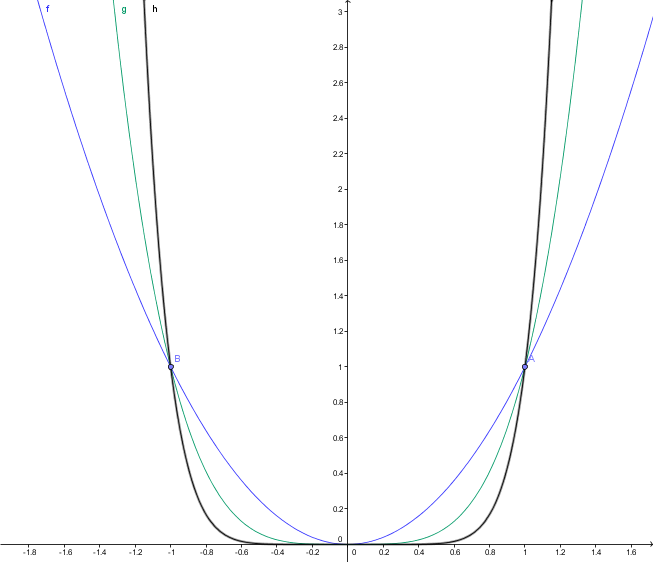
Es sind nun hier 3 Funktionen abgebildet: f(x)=x2, g(x)=x4 und h(x)=x8
Beim Betrachten dieser Grafen fällt dir sicher auf, dass sie symmetrisch zur y-Achse sind. Erinnern wir uns an das erste Kapitel, Satz 1.2.2. Daraus können wir folgendes ableiten: Ist nÎN gerade, so ist der Graf von f:x®xn symmetrisch zur y-Achse.
Wenden wir uns nun den Potenzfunktionen mit ungeraden, natürlichen Exponenten zu:
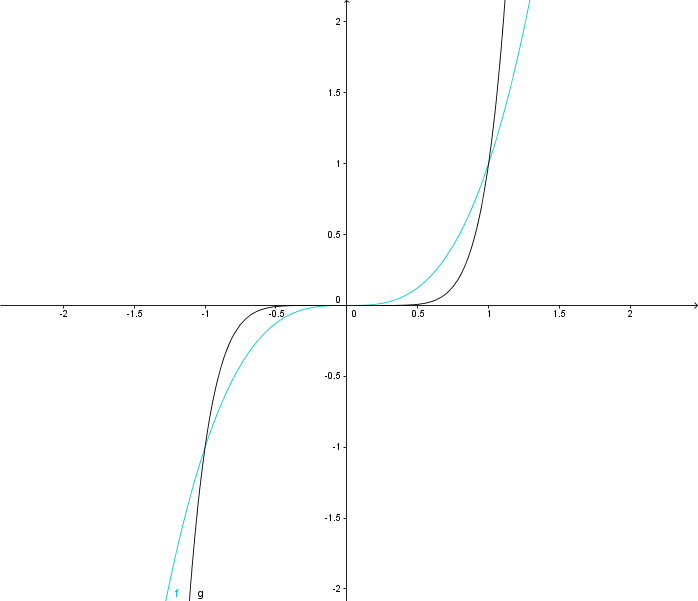
Hier sind 2 Funktionsgrafen abgebildet: f(x)=x3 und g(x)=x7
Bei dieser Art von Graf spricht man von einer Funktion, die symmetrisch zum Ursprung ist. Mittels Satz 1.2.2 erhalten wir folgende Regel: Ist nÎN ungerade, so ist der Graf von f:x®xn symmetrisch zum Ursprung.
Als nächstes wollen wir uns Funktionen vom Typ x®x-n für nÎN ansehen.
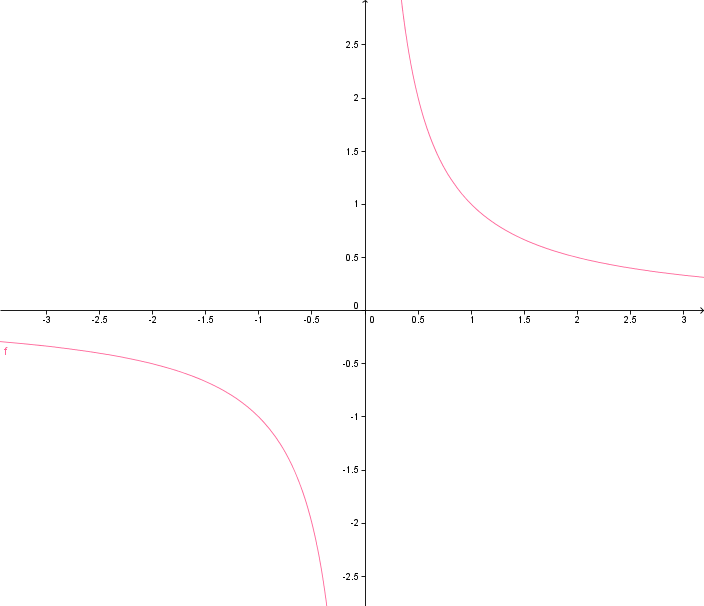
Dieser Graf zeigt f(x)=x-1
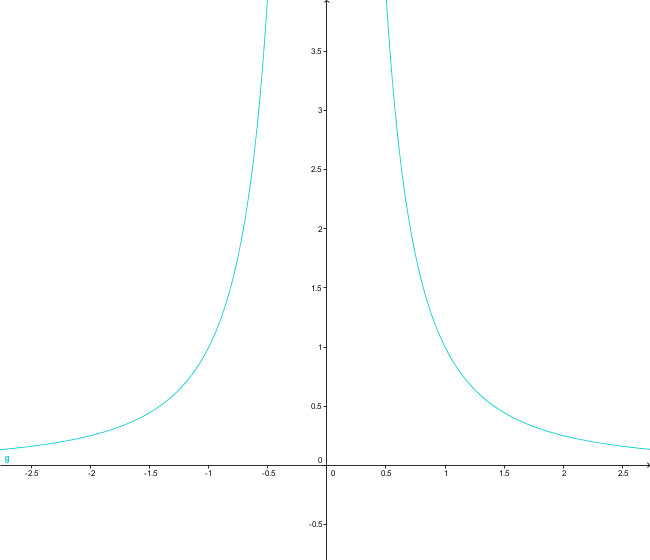
Dieser Graf zeigt g(x)=x-2
Offenbar gelten hier die selben Symmetrieregeln wie bei den positiven Exponenten. Trotzdem sehen die Grafen vollkommen unterschiedlich aus. Um den Unterschied etwas genauer unter die Lupe zu nehmen, schauen wir uns zum Abschluss noch das Monotonieverhalten an.
Satz 3.2.1: Für eine Potenzfunktion f:x®xn mit nÎN gilt:
(1) f ist in R0+ steng monoton steigend.
(2) f ist in R0- steng monoton fallend, falls n gerade ist, bzw. streng monoton steigend, falls n ungerade ist.
Übung: Beschreibe das Monotonieverhalten von f(x)=x-1 und g(x)=x-2
Lernstoff, Wiederholung
|
3.3 Übungsbeispiele zum sofort machen
|

 

|
Hier kannst du überprüfen ob du das Kapitel schon gut beherrschst.
Übung 1
Übung 2
Selfchecking Test
|
3.4 Beispiele zum Lösen am PC
|

  
|
Jetzt wollen wir das Gelernte gleich ausprobieren. Da ihr alle schon GeoGebra Profis seid, werden wir ein paar Funktionen eben dort näher untersuchen.
Übung 1: Visualisiere f(x)=x1 und g(x)=x3 mit GeoGebra. Färbe f(x) blau und g(x) rot. Finde die Schnittpunkte der beiden Funktionen und zeichne sie ein. Besprich in einer Gruppenarbeit mit deinem Nachbarn das Monotonieverhalten der beiden Funktionen und findet eine Erklärung für eure Beobachtungen.
Übung 2: Ergänze den GeoGebra-File, den du in Übung 1 angelegt hast um h(x)=x-1. Färbe h(x) grün. Vergleiche nun f(x) mit h(x) und besprich in einer Gruppenarbeit mit deinem Nachbarn die Unterschiede und was dir auffällt.
Übungsaufgaben
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



