|
1.1 einführungsbeispiel
|

  
|
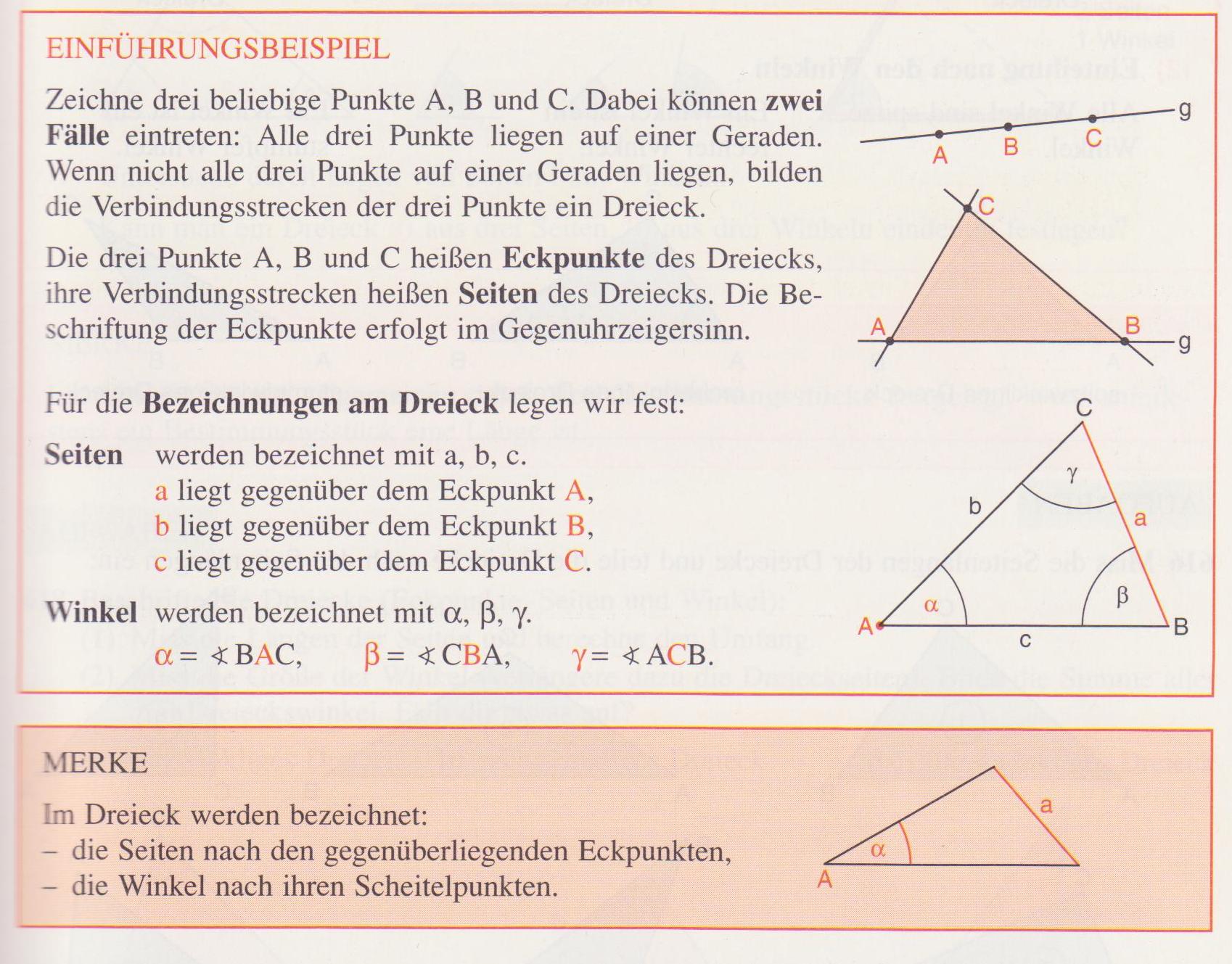
Quelle : “MATHEMATIK – Verstehen, Übern, Anwenden (Band 2)” (Ingrid Lewisch) (5. Auflage)
Lernstoff
|
|
1.2 Zeichne
|

 

|
Nachdem du dir das Einführungsbeispiel durchgelesen hast:
Zeichne nun selbst drei beliebige Punkte in deinem Heft und verbinde diese dann zu einem Dreieck.
Beschrifte die Seiten, die Eckpunkte und die Winkel des Dreiecks!
Übungsaufgabe
|
|
1.3 Einteilung der Dreiecke
|

  
|
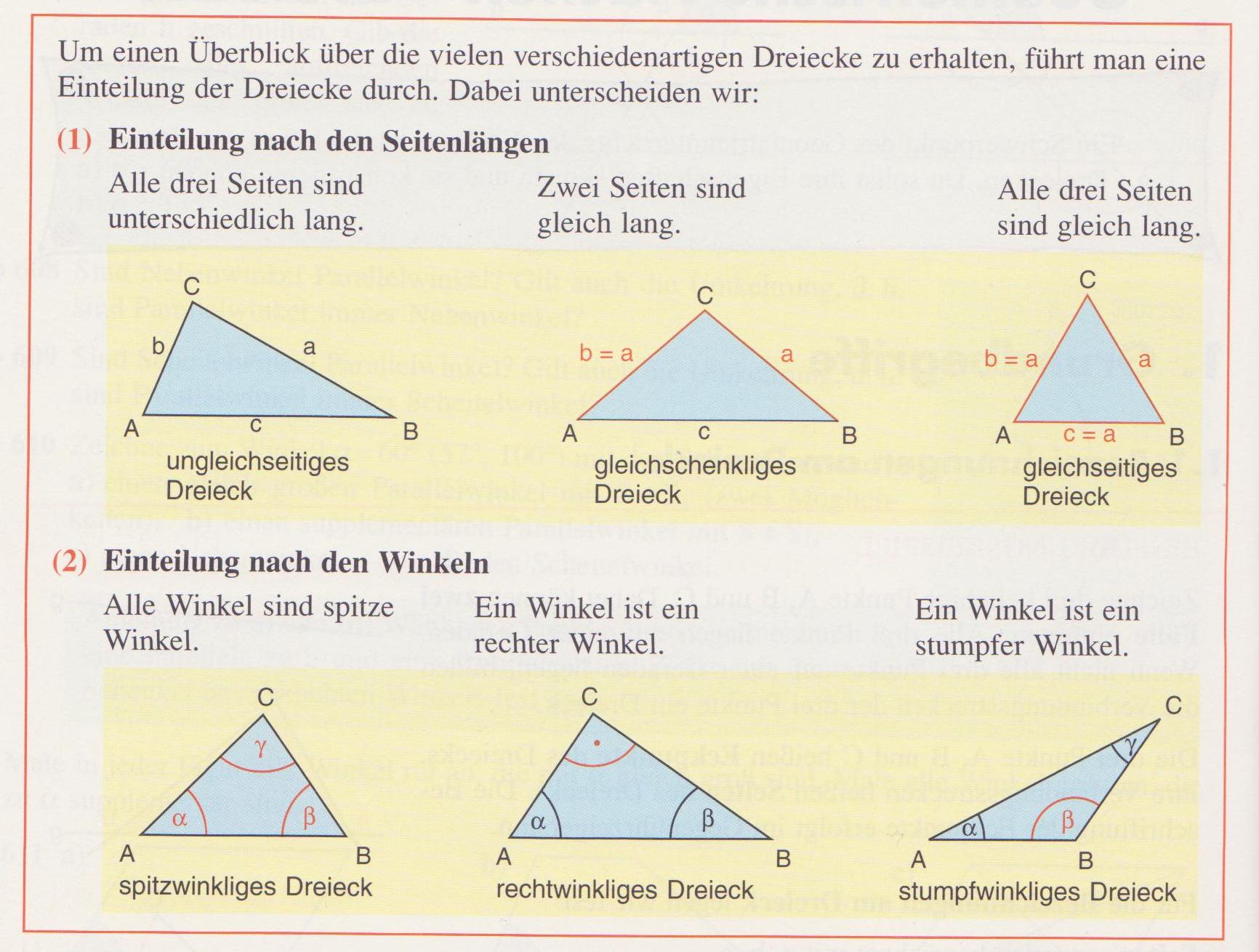
Quelle : “MATHEMATIK – Verstehen, Übern, Anwenden (Band 2)” (Ingrid Lewisch) (5. Auflage)
Lernstoff
|
|
1.6 Überlege
|

 

|

Quelle : “Das ist Mathematik 2” (Reichel – Humenbeger) (1. Auflage 2008)
Vertiefung
|
|
1.7 Zeichne das Dreieck in dein Heft
|

 

|
Ein Dreieck ist durch die Koordinaten seiner Eckpunkte im Koordinatensystem gegeben.
A (5/1), B (6/6), C (1/4)
a) Beschrifte das Dreieck. (Eckpunkte, Seiten, Winkel)
b) Miss die Längen der Seiten und berechne den Umfang.
c) Miss auch die Größe der Winkel. Bilde die Summe der drei Dreieckswinkel. Fällt dir dazu etwas auf?
Übungsaufgabe
|
|
1.8 Zeichne das Dreieck mit Hilfe von GeoGebra am Computer
|

 

|
Ein Dreieck ist durch die Koordinaten seiner Eckpunkte im Koordinatensystem gegeben.
A (2/1), B (6/6), C (2/6)
a) Beschrifte das Dreieck und miss die Längen der Seiten ab.
b) Miss auch die Größe der Winkel.
Gib deinen File in Moodle (Übungskurs: Geometrische Flächen - Dreiecke) ab.
Übungsaufgabe
|
|
1.9 Winkelsumme im Dreieck
|

  
|

Quelle : “MATHEMATIK – Verstehen, Übern, Anwenden (Band 2)” (Ingrid Lewisch) (5. Auflage)
Lernstoff
|
|
1.10 Begründe jeweils selbst:
|

 
|
Folgerung aus diesem Merksatz:
1) In einem Dreieck kann höchstens ein stumpfer Winkel auftreten.
2 ) In einem Dreieck kann höchstens ein rechter Winkel auftreten.
3) Sind in einem Winkel alle Winkel gleich groß, dann hat jeder dieser Winkel 60°.
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



