|
2.1 Kreisfunktionen am Einheitskreis
|

 

|
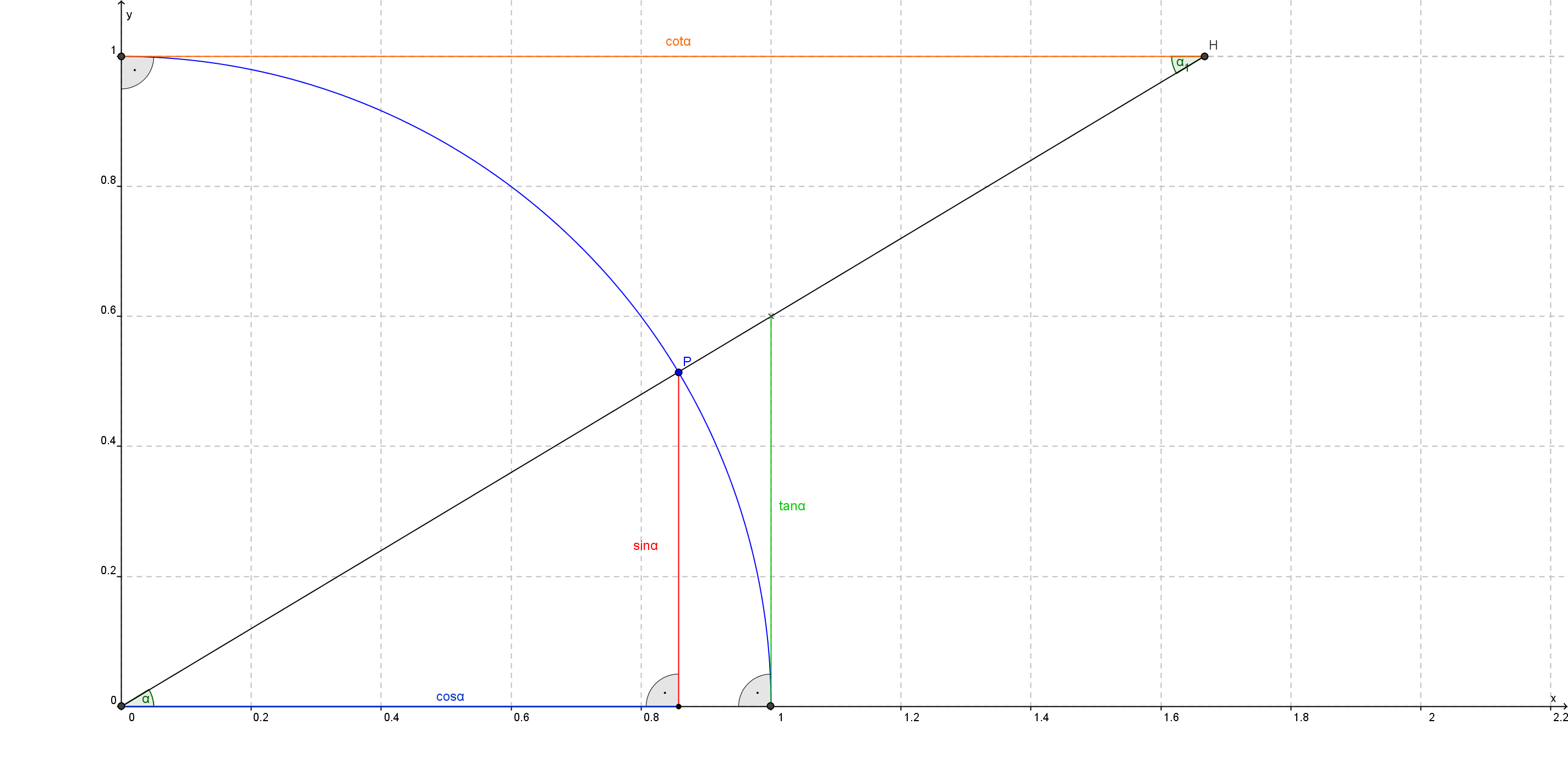
In diesen Graphen haben wir bereits viele Kreisfunktionswerte eingezeichnet, alle davon sind abhängig von den beliebig gewählten Winkel α (in diesem Fall 0<α<90°)
Im Vergleich zum rechtwinkligen Dreieck stellen wir fest, dass:
– der Sinuswert gleich der y-Koordinaten des Punktes P
– der Kosinuswert gleich der x-Koordinaten des Punktes P
ist.
Weiters stellen wir fest, dass das Verhältnis von dem Tangenswert zur Strecke O1 (die Gerade vom Nullpunkt zum Punkt 1) gleich dem Verhältnis vom Sinuswert zum Kosinuswert sein muss. D.h.:
tan(α) sin(α) sin(α)
————— = ————— -> tan(α)= —————
1 cos(α) cos(α)
Auch für den Kotangenswert lässt sich mittels Verhältnisse folgende Formel aufstellen:
cot(α) cos(α) cos(α)
————— = ————— -> cot(α)= —————
1 sin(α) sin(α)
Merke: sin(α)= y-Koordinate des zu α gehörigen Punktes P am Einheitskreis.
cos(α)= x-Koordinate des zu α gehörigen Punktes P am Einheitskreis.
Falls Nenner ≠0:
sin(α) cos(α) 1
tan(α)= ————— ; cot(α)= ————— ; cot(α)= —————
cos(α) sin(α) tan(α)
Auftrag: Übertrage die "blauen" Formeln mit Graph ins Schulübungsheft
|
|
2.2 Übungsbeispiel 1:
|

 

|
Gegeben: α=60°, 150°, 220°, 315°
a) Stelle die einzelnen Kreisfunktionswerte (cos, sin, tan) im Einheitskreis dar
b) Berechne die jeweiligen Werte
Lösung:
a)
b)
|
|
2.3 Beobachtung:
|

  
|
–Alle Sinus- & Kosinuswerte liegen zwischen -1 und 1
–Der Tangenswert kann gegen ±Unendlich gehen
Es ist vorteilhaft sich folgende wichtige und häufig auftretende Werte einzuprägen:
 Durch weitere Überlegungen am Einheitskreis stellen wir fest, das sich jeweilige Punktem und die dadurch resultierenden Werte,
sich nicht verändern, wenn man "eine weitere Runde dreht", also 360° addiert oder subtrahiert.
Für den Tangens gilt dies sogar für halbe Runden:
sin(α+k*2π)=sin(α)
cos(α+k*2π)=cos(α)
tan(α+k*π)=tan(α)
wobei k=0,±1,±2,±3,±4,...
π=180°
Man nennt diese ständigen Wiederholungen von Funktionswerten: Periodizität
Weiters gilt:
sin(-α)=-sin(α)
cos(-α)=cos(α
tan(-α)=-tan(α)
verdeutlicht durch folgende Graphik:
Durch weitere Überlegungen am Einheitskreis stellen wir fest, das sich jeweilige Punktem und die dadurch resultierenden Werte,
sich nicht verändern, wenn man "eine weitere Runde dreht", also 360° addiert oder subtrahiert.
Für den Tangens gilt dies sogar für halbe Runden:
sin(α+k*2π)=sin(α)
cos(α+k*2π)=cos(α)
tan(α+k*π)=tan(α)
wobei k=0,±1,±2,±3,±4,...
π=180°
Man nennt diese ständigen Wiederholungen von Funktionswerten: Periodizität
Weiters gilt:
sin(-α)=-sin(α)
cos(-α)=cos(α
tan(-α)=-tan(α)
verdeutlicht durch folgende Graphik:
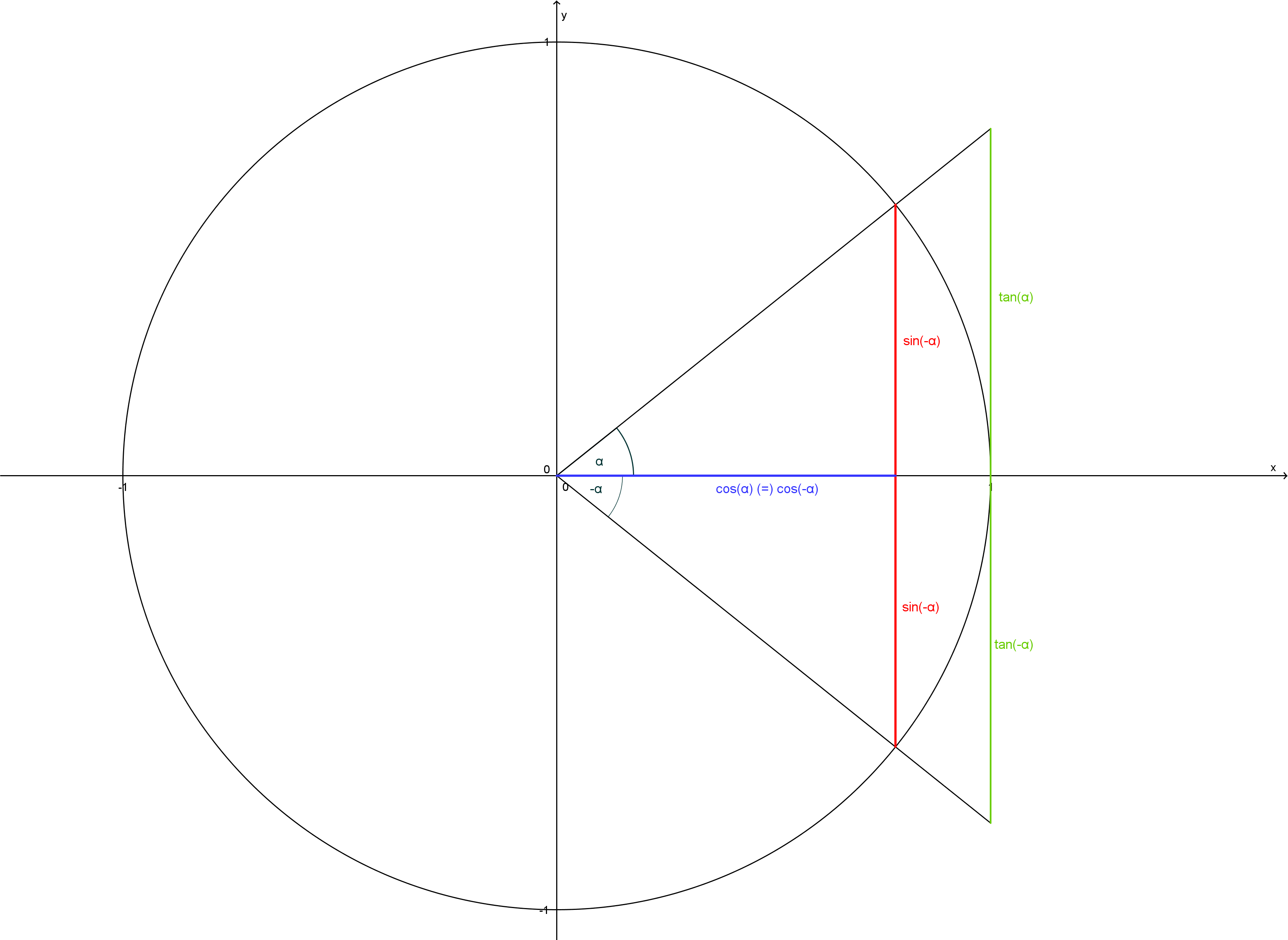
Auftrag: Übertrage zumindest die in blau geschriebenen Informationen in dein Schulübungsheft
|
|
2.4 Übungsbeispiel 2:
|

 

|
Überprüfe mittels zeichnen der Einheitskreise folgende Aussagen:
a) sin(180°-α)=sin(α)
b) cos(-α)=cos(α)
c) cos(α)=sin(α+90°)
Achtung: Wähle 0<α<90°
Lösung:
a)
b)
c)
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



