Mit den bis jetzt erreichten Wissensstand könnten wir naiverweise denken, dass gilt:
sin(α+β) = sin(α) + sin(μ)
Aber durch einsetzen von Zahlen merken wir schnell dass diese Gleichung nicht aufgeht.



Wir wissen bereits:



Für die anderen Formeln funktioniert die Herleitung ähnlich, aber dass ist Stoff der höheren Jahrgänge.
Für uns relevant sind die daraus resultierenden Formeln:


sin(α+(-)β)=sin(α)*cos(β) +(-) cos(α)*sin(β)
cos(α+(-)β)=cos(α)*cos(β) -(+) sin(α)*sin(β)

              tan(α) +(-) tan(β)
tan(α+(-)β)= ————————————————————
             1 -(+) tan(α)*tan(β)

für β=α gilt:

sin(2α)= 2*sin(α)*cos(β)
cos(2α)= cos²(α) - sin²(α)

           2*tan(α)
tan(2α)= ————————————
          1 - tan²(α)

Neben dem ersten Summensatz gibt es noch einen weiteren Summensatz.
Dieser macht es möglich, die Summe (Differenz) zweier Sinuswerte oder Kosinuswerte durch ein Produkt auszudrücken.
Auf seine Herleitung, die aus dem ersten Summensatz erfolgen kann, gehen wir nicht ein (Stoff der nächsten Jahrgänge).



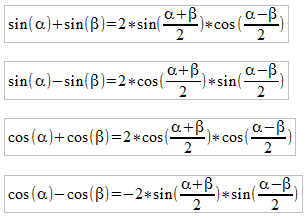Aufgabe: Übertrage die Summensätze (1&2) in dein Schulübungsheft.