|
1.1 Was passiert bei der Differentialrechnung?
|

 

|
Was wird dich erwarten?
-> Das Prinzip der Differentialrechnung geometrisch deuten...
-> Den Begriff "Ableitung einer Funktion f an einer Stelle x" verstehen...
-> Die Ableitung an einer Stelle x geometrisch deuten können...
-> Die Ableitung der wichtigsten Funktionen beherrschen...
-> Die wichtigsten Ableitungsregeln beherrschen...
-> Das Maximum von Kurven bestimmen können...
|  |
|
|
1.3 Das Tangentenproblem
|

  
|
|
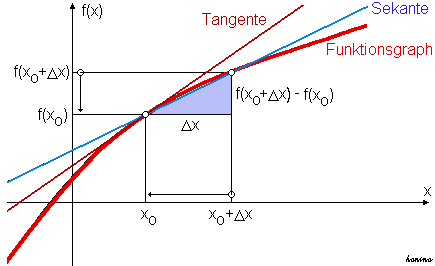
Man hat einen beliebigen Funktionsgraph (rot) gegeben. Weiters gibt es zwei beliebige Punkte x0 und (x0+Dx).
Zu diesen zwei x-Werten existieren (da die Funktion stetig sei) zwei y-Werte: f(x0) und f(x0+Dx).
Verbindet man diese zwei Punkte durch eine Gerade erhält man die sog. SEKANTE (lat. sekantere = schneiden).
Lässt man jetz den Punkt x0+Dx immer näher gegen den Punkt
x0 auf der x-Achse "rutschen", dh. Dx -> 0 gehen, erhält man (wenn der Limes gebildet wird) eine TANGENTE im Punkt x0. (lat. tangentere = berühren).
Durch die Bildung des Limes erhält man die STEIGUNG DER TANGENTE im Punkt x0
|
Formal sieht das ganze so aus:
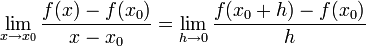
Dieser Formalismus wird auch als f '(x0) oder die 1.te ABLEITUNG der Funktion bezeichnet.
Die Steigung der Tangente bzw. die Ableitung der Funktion wird weiters noch sehr wichtig sein...
MERKE: Durch Bildung der 1.ten Ableitung der Funktion erhält man die Steigung der Tangente in einem beliebigen Punkt x!
Schreibe kurz und grundelegend die Grundgedanken der Differentailrechnung in dein Schulheft!
|
1.5 Historischer Rückblick ....
http://http://de.wikipedia.org/wiki/Differentialrechnung#Geschichte
|

 

|
Die Differentialrechnung haben unabhängig voneinander der deutsche Philosoph Gottfried wilhelm Leibniz (linkes Bild) (1646-1716) und der englische Naturforscher Isaac Newton (rechtes Bild) (1643-1727) entwickelt.
Für Leibnitz war das Tangentenproblem der Ausgangspunkt, dür Newton der Geschwindigkeitsbegriff (hier in diesem Lenrpfad keine nähere Erläuterung dazu).
Auch die gebräuchlichen Bezeichnungen gehen auf Leibniz zurück.
Wenn du dich näher für das Historische interessierst kannst du näheres auf Wikipedia nachlesen.. (siehe dazu Link ganz oben)
Bei Interesse...
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



