|
3.1 Die Ableitung der Winkelfunktionen
|

  
|
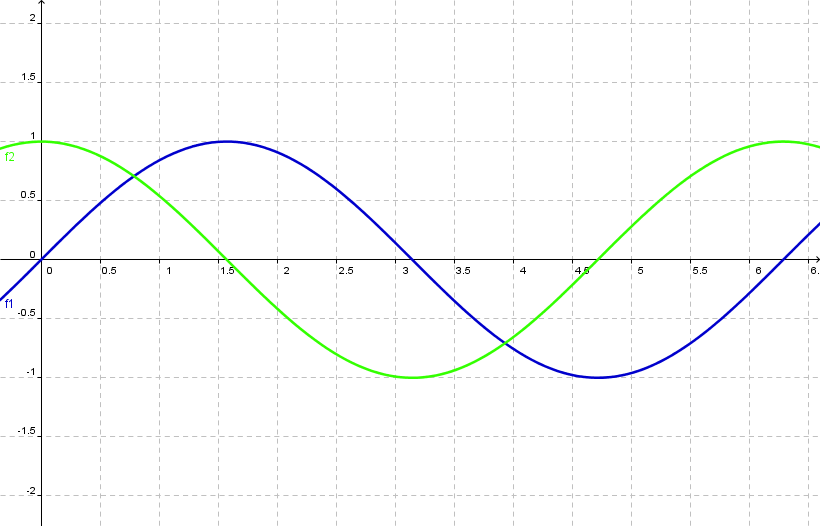
Wir werden uns in diesem Abschnitt mit den drei Winkelfunktionen:
f(x) = sin(x)
f(x) = cos(x)
| 
|
|
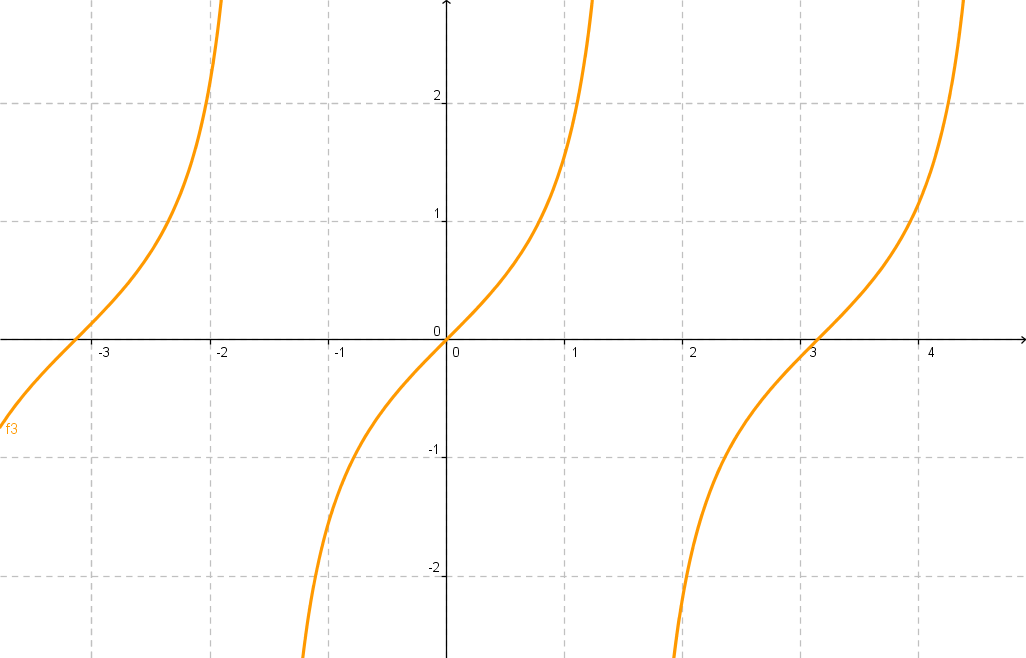
f(x) = tan(x)
| 
|
und deren erster Ableitung beschäftigen.
Die Ableitungsregeln für die Sinus- und Cosinusfunktion sehen folgendermaßen aus:
f(x)= sin(x)
f '(x)= cos(x)
|
f(x)= cos(x)
f '(x)= -sin(x)
|
FRAGE: Kannst du irgendeine Beziehung zwischen den beiden Funktionen erkennen?
Die Ableitung der Tangensfunktion sieht folgendermaßen aus:
f(x)= tan(x)
f '(x)= 1+tan(x) oder = 1 / cos2(x)
FRAGE: Ist die erste Ableitung der Tangensfunktion überall definiert?
Zeichne dir zur Wiederholung die drei Winkelfunktionen in dein Heft und schreibe die Ableitungsregeln dazu!
|
|
3.2 Die Produktregel
|

 

|
Hat man ein Produkt von zwei Funktionen u(x) · v(x) muss man die Produktregel zum bestimmen der Ableitung verwenden!
Die Produktregel lautet: (u · v) = u'(x) · v(x) + u(x) · v'(x)
Bsp: Es ist die Funktion f(x)= 3x² · ex (3x² = u(x),ex = v(x)) gegeben.
Nach der Produktregel wird gerechnet: f '(x) = 6x · ex + 3x² · ex
Schreibe die Produktregel in dein Schulheft!
|
|
3.4 Die Quotientenregel
|

 

|
Hat man einen Quotienten von zwei Funktionen u(x) / v(x) muss man die Quotiententregel zum bestimmen der Ableitung verwenden!
Die Quotientenregel lautet: (u / v)' = (u' · v - u · v') / v²
Bsp: Es ist die Funktion f(x) = sin(x) / x gegeben.
Nach der Quotientenregel wird gerechnet: (f '(x) = cos(x) · x - sin(x)· 1) / x²
Schreibe die Quotientenregel in dein Schulheft!
|
|
3.5 Die Kettenregel
|

  
|
Die Kettenregel muss verwendet werden wenn man eine verkettete Funktion hat; man sagt auch einen innere und eine äußere Funktion.
So eine Funktion ist z.B.: f(x) = cos(2x)
An diesem Beispiel ist cos(..) die äußere Funktion und 2x die innere Funktion
Die Kettenregel lautet: f '(x) = Ableitung der äußernen Funktion · Ableitung der inneren Funktion
(oder auch kurz: äußere mal innere Ableitung)
Bsp: Es ist die Funktion f(x) = cos(2x) aus dem obigen Text gegeben.
Nach der Kettenregel wird gerechnet: f '(x) = -sin(2x) · 2
ACHTUNG!: Das Anwenden der Kettenregel ist eine häufige Fehlerquelle, da oft leicht ÜBERSEHEN wird dass man die innere Ableitung auch bilden muss!
Schreibe die Kettenregel in dein Schulheft!
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



