|
4.1 Noch ein bisschen benötigstes Werkzeug...
|

 
|
Wir brauchen für die Bestimmung der Extremwerte von Funktionen noch HÖHERE ABLEITUNGEN
Wenn die 1.te Ableitung f '(x) wieder eine differenzierbare Funktion ist, so erhält man durch nochmaliges Differenzieren die 2.te Ableitung, f ''(x) etc.
Also:
(f '(x))' = f ''(x)
(f ''(x)' = f '''(x) etc.
Man nennt f ''(x), f '''(x), ... die HÖHEREN ABLEITUNGEN .
|
|
4.2 Die Bestimmung des Extremwertes einer Funktion
|

  
|
Unter Extremwert einer Funktion versteht man ein (relatives) Maximum oder Minimum einer Funktion. Um ein solches bestimmen zu können
brauchen wir nun die bereits gelernten Ableitungen.
Die Idee: Die 1.te Ableitung einer Funktion gibt die Steigung der Tangente in einem beliebigen Punkt x0 (sofern die Funktion
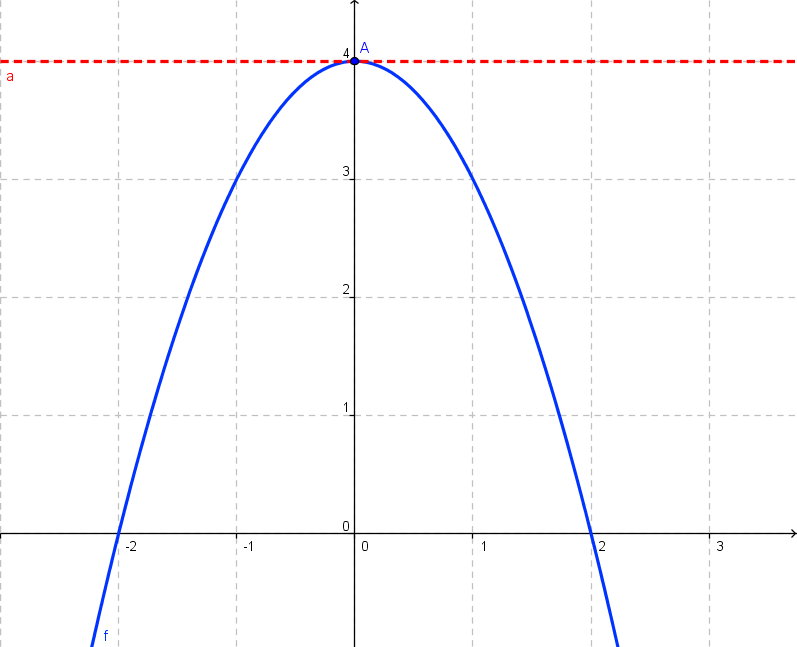
in diesem Punkt stetig ist) an. Wenn man sich jetzt vorstellt dass an einem Extremwert einer Funktion die Tangente genau horizontal liegt (siehe Graphik),
kann man daraus folgern dass die Steigung der Tangente genau = NULL sein muss! (horizontal = "keine" Steigung -> f '(x) = 0 )
Versuchen wir das ganze gleich an einem Beispiel anzuwenden:
Gegeben sei die Funktion f(x) = -x²+4.
(Die Funktion ist zumindest 2-mal stetig differenzierbar.-> Vorraussetzung dass man bis zur 2.ten Ableitung berechnen kann)
Wir bilden nun die 1.te Ableitung der Funktion f(x):
Durch anwenden der Potenzregel erhalten wir: f '(x) = -2x
Wir wollen nun wissen WO die Funktion eine horizontale Tangente besitzt, und setzen somit die 1.te Ableitung = 0
f '(x) = -2x = 0 -> x = 0
somit haben wir erhalten dass bei x = 0 ein Punkt auf der Kurve existiert wo eine horizontale Tangente (=EXTREMWERT) vorliegt.
Eingesetzt in die Ausgangsgleichung erhalten wir: f(x) = -0² + 4 = 4
dass bei x = 0 und bei y = 4 dieser Extremwert vorliegt.
|
|
Übe dazu ein paar gestellte Beispiele aus dem Schulbuch!
|
|
4.3 Last but not least.....
|

  
|

|
ALLES KLAR SOWEIT?
Ansonsten:
S C H Ö N E
F E R I E N !
|
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



