|
1.1 Wichtige Fakten
|

 
|
In der Geometrie unterscheidet man zwischen
dem Kreis/der Kreislinie

und der Kreisfläche

Der Kreis ist der Rand der Kreisfläche.
Alle Punkte der Kreislinie haben vom Mittelpunkt M den selben Abstand, nämlich den Radius r.

Der Durchmesser ist doppelt so lang wie der Radius.

Der Umfang ist proportional zum Durchmesser.
Je größer der Durchmesser, desto größer ist der Umfang.
Der Proportionalitätsfaktor ist die Zahl π.


Lernstoff
|
|
1.2 Kreuzzahlenraetsel
|

 


|
Fülle das Kreuzzahlenrätsel aus und notiere deine Rechenschritte im Lerntagebuch.
Rätsel
Eintrag in das Lerntagebuch
|
|
1.3 Die Zahl Pi
|

 
|
Die Zahl π ist eine irrationale Zahl, also eine nicht periodische Dezimalzahl mit unendlich vielen Dezimalstellen.
Man kann heute mit leistungsfähigen Computer viele tausende Dezimalstellen von π berechnen.
Die Zahl π ist das für alle Kreise gleichbleibende Verhältnis vom Kreisumfang zum Kreisdurchmesser.


Lernstoff
|
|
1.4 Berechnung der Zahl Pi
|

 
|
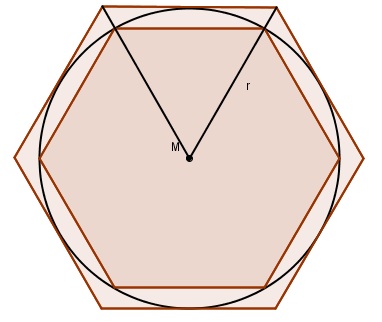
Das Bild deutet eine Methode an, wie man die Zahl π näherungsweise berechnen kann:
Einem Kreis mit dem Radius r wird je ein regelmäßiges n-Eck (z.B. ein Sechseck) eingeschrieben.
Mit Hilfe der entsprechenden Dreiecke kann man den Umfangang un des eingeschriebenen bzw. u2n des umgeschriebenen n-Ecks berechnen.
So ist z.B. 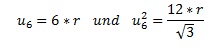
Du kannst das mit Hilfe gleichseitiger Dreiecke begründen.
Für den Umfang u des Kreises erhältst du demnach unter und obere Schranke.
u6 < u< u2n.
Aus dem regelmäßigen Sechsecken folgt:
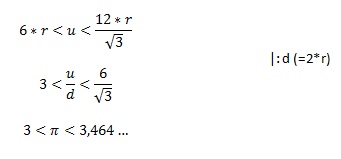
Je größer die Anzahl n der Ecken ist, desto besser nähert sich un und u2n dem tatsächlichen Kreisumfang u an.
Für die Zahl π gilt dann:
π = 3,141...
Für Überschlagsrechnungen verwendet man meist den Näherungswert π ≈ 3, beim händischen Rechnen π ≈ 3,14
Lernstoff
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



