|
3.1 Definitionen
|

 

|
Ist a∈ℝ+, so nennt man jene nichtnegative reelle Zahl, deren n-te Potenz gleich a ist, die n-te Wurzel aus a und bezeichnet sie mit
n√a.
Symbolisch heißt das:
n√a=x ⇔ xn=a ∧ x≥0
Man bezeichnet a als Radikand und n als Wurzelexponent.
Bemerkung: Für n=2 schreibt man üblicherweise nur √a und für n=1 ergibt sich 1√a=a.
Lernstoff
|
|
3.2 Rechenregeln für Wurzeln
|

  
|
Für alle a∈ℝ+, alle n∈ℤ* und alle k∈ℤ* gilt:

Für alle a,b∈ℝ+ und alle n∈ℤ* gilt:

Für alle a∈ℝ+ und alle m,n∈ℕ* gilt:
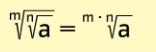
Für alle a∈ℝ+, alle k,n∈ℕ* und alle m∈ℤ gilt:
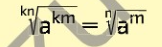
Lernstoff
|
|
3.3 Veranschaulichung
|

 

|
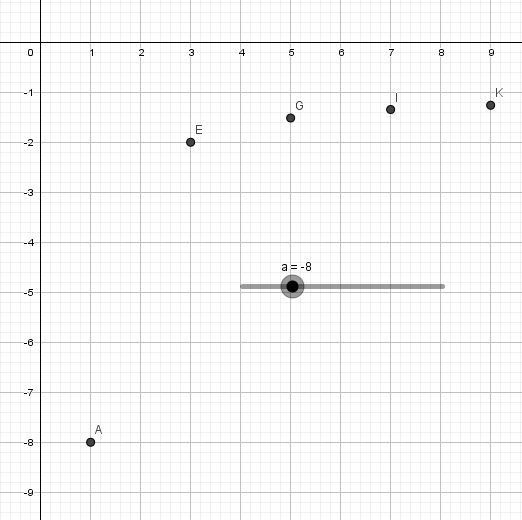
In der folgenden Grafik kannst du sehen das die n-te Wurzel für manche n mit einer bestimmten Eigenschaft sehrwohl lösbar sind. Der Radikand in der Grafik ist mit -8 gewählt.
Welche Bedingung muss der Wurzelexponent (welcher zu den Punkten passend auf der waagrechten Achse angegeben ist) erfüllen damit die n-te Wurzel berechenbar ist. (Tipp: Die Grafiken in Kapitel 1 und 2 könnten hilfreich sein)
Hier wieder der Link zur GeoGebra-Datei.
GeoGebra-Visualisierung
Experimentiere wieder mit dem Schieberegler und achte insbesondere darauf was passiert wenn sich der Radikand in den Intervallen (-1;1), (-∞;-1) und (1;∞)bewegt.
Quadratwurzel
In der nachfolgenden Grafik siehst du den Graphen zu der wohl am häuigsten verwendeten Wurzel.
Die Quadratwurzel mit Wurzelexponent = 2.
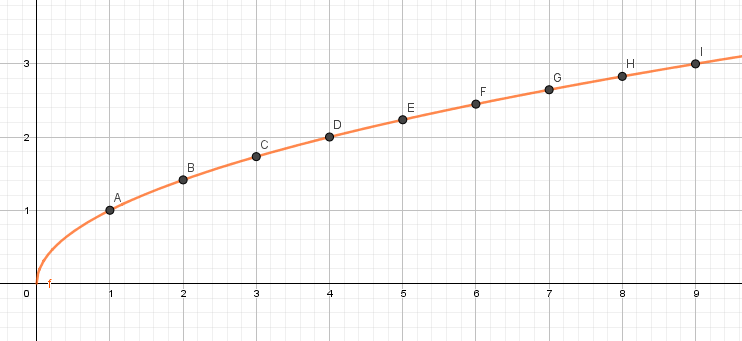
Achtung: Auf der waagrechten Achse sind nun nicht mehr die Wurzelexponenten sondern die Radikanden.
Vertiefung
|
|
3.4 Übungen
|

 

|
Auch hier wieder ein paar Aufgaben zum üben.
Übungsblatt
Übungsaufgaben
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



