|
5.1 Definitionen
|

 

|
Sei a∈ℝ+ und r∈ℝ.
Unter ar versteht man jene Zahl, die zwischen allen Zahlen ax
mit rationalem x<r und allen Zahlen ay mit rationalem y>r liegt.
Lernstoff
|
|
5.2 Rechenregeln für Potenzen mit Exponenten aus ℝ
|

  
|
Für alle a∈ℝ+ und alle x,y∈ℝ gilt:
- ax·ax=ax+y
- ax/ay=ax-y
- (ax)y=ax·y
Für alle a,b∈ℝ+ und alle x∈ℝ gilt:
- (a·b)x=ax·bx
- (a/b)x=ax/bx
Für alle a∈ℝ+ und alle x∈ℝ+ gilt:
- a>1 ⇒ ax>1
- 0<a<1 ⇒ 0<ax<1
Lernstoff
|
|
5.3 Veranschaulichung
|

 

|
Diese Definition wirkt sehr kompliziert aber einfach gesagt: Man beschränkt die Potenz auf einen Wert zwischen 2 berechenbaren Potenzen und je näher man zusammenrückt desto genauer kann man den Wert bestimmen.
In der Grafik ist die Basis 2 und der zum Punkt A zugehörige Exponent ist π/2.
Die Exponenten von den beiden anderen Punkten sind (π/2)-i und (π/2)+i.
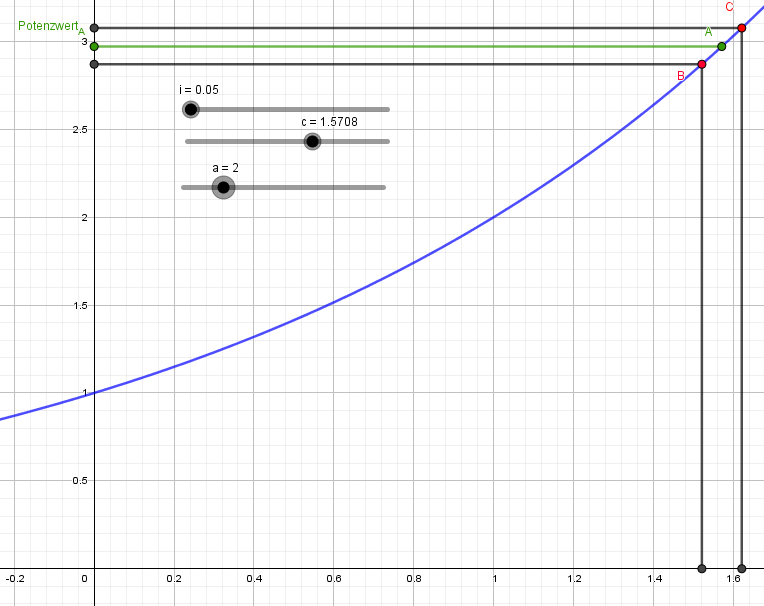
Bemerkung: Die Exponenten von den beiden Punkten neben A sind ebenso irrationale Zahlen. Die Annäherung sollte aber mit rationalen Exponenten erfolgen.
Die Exponenten sind nur aufgrund der leichteren Umsetzung der Veranschaulichung so gewählt.
Hier ist wie üblich wieder das zugehörige GeoGebra-File, mit dem du wieder herumprobieren kannst und dir hoffentlich die Definition veranschaulicht.
GeoGebra-Datei zur Definition von Potenzen mit reellem Exponent
Vertiefung
|
|
5.4 Übung
|

 

|
Hier eine sind Aufgaben zum berechnen von Potenzen mit irrationalem Exponent.
Übungsblatt
Übungsaufgaben
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



