|
1.1 Wiederholung
|

 

|
► WAS IST EIN VEKTOR ?
Ein Vektor beschreibt eine Verschiebung eines Punktes A, der auf einen Punkt B abgebildet wird. Dies schreibt man so :
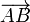 Grafisch wird ein Vektor durch einen Pfeil dargestellt, der vom Punkt A zum Punkt B zeigt. Man sagt: „Der Vektor
Grafisch wird ein Vektor durch einen Pfeil dargestellt, der vom Punkt A zum Punkt B zeigt. Man sagt: „Der Vektor 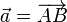 bildet A auf B ab“, oder: „Der Vektor bildet A auf B ab“, oder: „Der Vektor 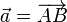 verbindet A und B.“
Der Punkt A ist in diesem Fall der Startpunkt und B die Spitze oder der Endpunkt des Vektorpfeils. Der Abstand der beiden Punkte wird "Länge" oder "Betrag" des Vektors genannt. verbindet A und B.“
Der Punkt A ist in diesem Fall der Startpunkt und B die Spitze oder der Endpunkt des Vektorpfeils. Der Abstand der beiden Punkte wird "Länge" oder "Betrag" des Vektors genannt.

Quelle: Wikipedia
In der Geometrie bezeichnet man einen Vektor auch als Parallelverschiebung, die in der Ebene oder im Raum stattfinden kann. Pfeile, die gleich lang, parallel und gleich gerichtet sind, stellen dieselbe Verschiebung dar und somit den gleichen Vektor.
Zum Beispiel beschreibt das Bild unterhalb eine Vektorverschiebung um 4 Einheiten nach rechts und 1 Einheiten nach oben. Erkennbar ist dies durch die Pfeile von A nach A‘, B nach B‘ und C nach C‘.
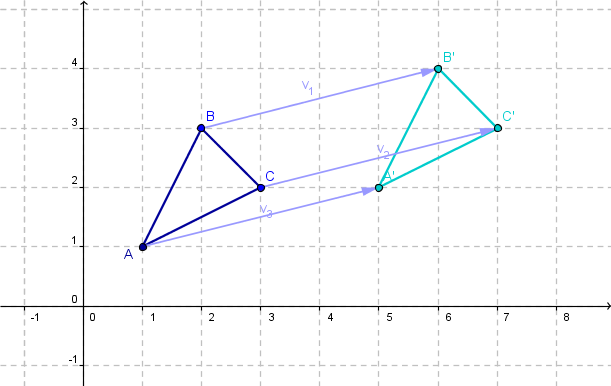
kurze Anmerkung
Man kann einen Vektor in Zeilen- oder Spaltenform darstellen.

► Kleine Übung
Lückentext
|
|
1.2 WH2
|

 
|
► DER BETRAG EINES VEKTORS
Unter dem Betrag eines Vektors versteht man die Länge eines Pfeils. Kennt man die x- und y-Komponente eines Vektors, so kann man daraus die Länge des Vektors ermitteln.
Erklärung zu Betrag eines Vektors
► Kleine Übung
Zuordnungsübung
|
|
1.3 WH3
|

 
|
► DIE VEKTORADDITION
Die Vektoraddition ist eine Aneinanderreihung mehrerer Verschiebungen. Grafisch wird eine Vektoraddition wie unten dargestellt angezeigt. Die Spitze (Ende) des ersten Vektors wird an den Schaft (Anfang) des zweiten Vektors gesetzt.
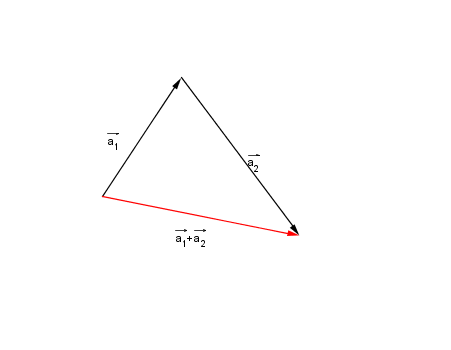 Rechnerisch schaut das ganze so aus:
Rechnerisch schaut das ganze so aus:
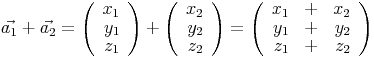
► Kleine Übung
Rechenregeln
|
|
1.4 WH4
|

 
|
► DAS VEKTORIELLE PRODUKT
• Multipliziert man einen Vektor mit einer Zahl, so ist das Ergebnis wieder ein Vektor.
• Multipliziert man zwei Vektoren, so ist das Ergebnis eine Zahl, die man auch Skalar nennt.
• Es gibt aber auch eine Vektormultiplikation oder das vektorielles Produkt. Hier ist das Ergebnis auch wieder ein Vektor. Diese Art der Multiplikation nennt man manchmal auch Kreuzprodukt
Das Skalarprodukt

Das Kreuzprodukt berechnet man so:

Quelle: Grafiken
Das vektorielle Produkt zweier Vektoren hat den Wert Null, wenn wenigsten einer der beiden Vektoren der Nullvektor ist oder wenn die beiden Vektoren parallel sind.
Allerdings, wenn das Vektorprodukt zweier Vektoren, von denen keiner der Vektoren gleich Null ist, so sind sie parallel.

|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



