|
2.1 ► ALLGEMEINE FORM
|

 

|
■ für die Geradengleichung
y = kx + d
Die x und y Werte stammen von einem bliebigen Punkt der Gerade g, k ist die Steigung und d der Abstand vom Koordinatenursprung auf der y-Achse nach oben.
grafisch kann man sich das so vorstellen:

■ der Ebene
ε : a * x + b * y + c * z = d
|
|
2.2 ► PARAMETERFORM
|

 

|
■ für die Geradengleichung
R und S sind zwei beliebige Punkte in der Ebene.
Setzt man in der Gleichung X = R + µ * RS für µ verschiedene Zahlen ein, so erhält man für X immer einen Punkt auf der Geraden durch R und S. Man kann aber auch zu jedem Punkt auf der Geraden eine entsprechende Zahl µ finden. µ wird als Parameter bezeichnet.
Daraus folgt, dass die Parameterform der Gerade wie folgt lautet:

Manchmal ist allerdings von einer Gerade g ein Punkt R und ein Richtungsvektor a gegeben, so lautet die Gleichung der Geraden in Parameterform:
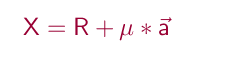
Kleine Übung zu Geraden Hinweis: Klicke auf Arbeitsblatt :-)
■ der Ebene
Eine Ebene wird durch einen Punkt und zwei Richtungsvektoren 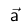 und und 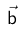 bestimmt. Daher enthält die Gleichung der Ebene zwei Parameter . In diesem Fall α und β.
bestimmt. Daher enthält die Gleichung der Ebene zwei Parameter . In diesem Fall α und β.
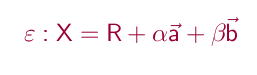
Hilfe für das Verständnis !
|
|
2.3 ► NORMALVEKTORFORM
|

 

|
■ für die Geradengleichung
Es sei eine Gerade g, ein Punkt R und ein Normalvektor n gegeben. Der Vektor n steht normal auf alle Richtungsvektoren RX (X ist ein beliebiger Punkt auf der Geraden) diesern Gerade g. Ihr Skalarprodukt ist daher 0.
® n*RX = 0
® n*(X - R) = 0
® n*X - n*R = 0
Die Gleichung der Geraden in Normalvektorform lautet daher:
g: n * X = n * R

Ein Beispiel zur Veranschaulichung:

Durch Ausmultiplizieren erhält man die Normalform der Geradengleichung: 2x - y = 5
Die Koordinaten des Normalvektors sind also die Koeffizienten von x und y in der Normalform!
Eine Gerade im Raum kann man nicht in der Normalvektorform darstellen, weil es im Raum keinen eindeutigen Normalvektor gibt.
■ der Ebene
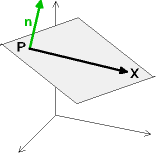
Für die Normalvektorform der Ebene braucht man einen Punkt der Ebene, sowie einen Normalvektor n. Die Gleichung erhält man dann analog zur Geradengleichung.
e : n * X = n * R
Ein Beispiel zur Veranschaulichung:

Durch Ausmultiplizieren erhält man die Normalform der Geradengleichung: 3x + 2y - z = 4
| 
|
|
|
2.4 ► DIE HESSE´SCHE NORMALFORM
|

 

|
Wird der Normalvektor in der Normalvektorform durch einen Einheitsvektor ersetzt, so gelangt man zu HESSE´schen Normalform
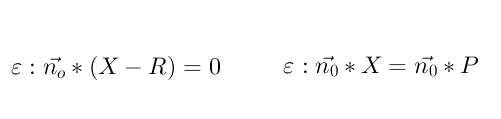
Anwendung
Für Interessierte :-)
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



