|
3.1 ► Lage eines Punktes zu einer Geraden bzw. Ebene
|

 

|
■ P Î g

2 = 5 + 8*g ® g = - 3/8
-1 = 3 - g ® g = 4
3 = 4 + 2*g ® g = -1/2
in diesem Fall ist P Ï g, da hier g unterschiedlich ist. Hätte g immer den gleichen Wert, dann wäre P Î g
|
 |
■ P Î e
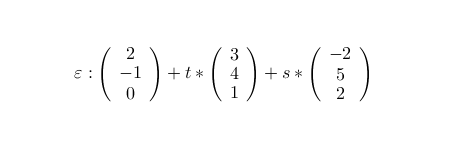

ε in Normalform bringen:

ε : 3x - 8y + 23z = 14
Nun überprüfen wir, ob der Punkt (2|-1|3) auf der Ebene liegt.
3 * 2 + 8 * (-1) + 23*3 = 14
83 ¹ 14 ® P Ï e
Wäre die Gleichung richtig, dann würde P Îe sein.
|
 |
|
|
3.2 ►Lagebeziehung von 2 Geraden
|

 

|
2 Geraden können zueinander parallel, identisch oder windschief sein oder sie schneiden sich.
· Nun überprüfen wir auf Parallelität:

g || h
g und h sind parallel, da der Richtungsvektor von h ein vielfaches vom Richtungsvektor g ist.
· Nun überprüfen wir auf Identität :
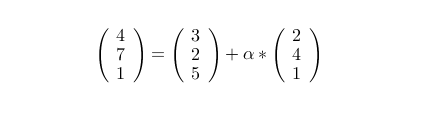 4 = 3 + a * 2 a = 1/2
4 = 3 + a * 2 a = 1/2
7 = 2 + a * 4 a = 5/4
1 = 5 + a * 1 a = -4
g ist nicht identisch mit h , da der Parameter nicht gleich ist.
· Nun überprüfen wir ob sie sich schneiden :
3 + a * 2 = 4 + b * 4
2 + a * 4 = 7 + b * 8
5 + a * 1 = 1 + b * 2
Wenn man bei der Überprüfung keinen Schnittpunkt erhält und die Geraden weder identisch noch parallel sind, dann nennt man sie windschief.
|
 |
|
|
3.3 ►Lagebeziehung von g und e
|

 

|
<


Þ -3x -16y + z = 14

e -3x -16y + z = 14
3 *( -1 + 2s) + 16 * (2 + s) - (3 + 3s) = -14 ® 19s = -40 ® s = -40/19
|
 |
Da wir für den Parameter s einen Wert erhalten haben, weiß man, dass sich die Gerade mit der Ebene schneidet. Würde s wegfallen, ist ein Schnitt ausgeschlossen. Würde die Gleichung z.B 12 = 40 ergeben, dann wäre die Gerade parallel zur Ebene. Würde das Ergbenis z.B 40 = 40 sein, dann wären die Gerade und die Ebene ident.
Nun berechnen wir den Schnittpunkt:

Hilfreiche Informationen und Beispiele !
|
|
3.4 ►Lagebeziehung zwischen 2 Ebenen
|

 

|
<

e1: 6x - 5y - 4z = 19
e2 y=0
wähle z = g
6x - 5y = 19 + 4 * g
y=0
6x = 19 + 4* g
x = 19/6 + 4/6 * g
y = 0 + 0 * g
z = 0 + 1 * g4
Die Schnittgerade
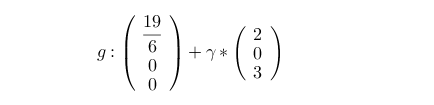
Wäre der Normalvektor der einen Ebene ein Vielfaches der zweiten Ebene, dann wären die beiden Ebenen parallel
|
 |
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



