|
2.1 Die Ableitung an der Stelle x
|

  
|
Wie bereits erklärt, nennt man für den Punkt x1 den Limes
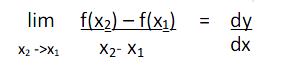 den Differentialquotienten bzw. die Ableitung der Funktion f(x) an der Stelle x1.
Wir können auch sagen:
Für einen Punkt x heißt der Limes
den Differentialquotienten bzw. die Ableitung der Funktion f(x) an der Stelle x1.
Wir können auch sagen:
Für einen Punkt x heißt der Limes
 die Ableitung der Funktion f(x) am Punkt x. Man schreibt für diese Ableitung am Punkt x
auch:
die Ableitung der Funktion f(x) am Punkt x. Man schreibt für diese Ableitung am Punkt x
auch:
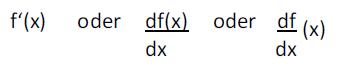 Schreibe diese Definition in dein Schulübungs-Heft!
Schreibe diese Definition in dein Schulübungs-Heft!
Definition (Lernstoff)
|
|
2.2 Ableitungsregeln
|

 

|
Natürlich wäre es umständlich und meistens auch schwierig, diesen Limes jedesmal
auszurechnen. Es gibt jedoch Regeln, wie die Ableitungen verschiedener Funktionen
aussehen.
Ein Beispiel: Für die Funktion f(x)= xq gilt:
f‘(x)= q*xq-1
Wenn also f(x)=x³
Dann gilt:
f‘(x) = 3x²
Ihr solltet diese und andere Ableitungen bereits kennen.
Eine Liste verschiedener Ableitungsfunktionen findest du in deinem Formelheft, oder
(etwas genauer) hier:
Liste von Ableitungsfunktionen
Ebenso solltet ihr bereits die Ableitungsregeln durchgenommen haben. Auch diese findet
ihr in eurem Formelheft oder (mit ein paar Beispielen) unter folgenden Links:
Faktorregel
Summenregel
Produktregel
Quotientenregel
Schau dir die Regeln und die angeführten Beispiele durch. Du musst nicht alle
Ableitungsfunktionen und Regeln auswendig können, doch empfiehlt es sich, sie immer
parat zu haben!
Regeln
|
|
2.3 Übungen zu den Ableitungsregeln
|

 

|
 Es wird nun Zeit, dein Wissen zu testen. In den folgenden Links stellt dir die Sphinx wieder
Rätsel. Du sollst Ableitungen ihren ursprünglichen Funktionen zuordnen. Wenn du die
Ableitungsregeln nicht gut genug auswendig weißt, kannst du natürlich in den obigen
Links nachsehen!
Viel Glück!
‘Nun, denn Reisender. Lass uns beginnen‘:
Polynomfunktionen
Winkelfunktionen
Es wird nun Zeit, dein Wissen zu testen. In den folgenden Links stellt dir die Sphinx wieder
Rätsel. Du sollst Ableitungen ihren ursprünglichen Funktionen zuordnen. Wenn du die
Ableitungsregeln nicht gut genug auswendig weißt, kannst du natürlich in den obigen
Links nachsehen!
Viel Glück!
‘Nun, denn Reisender. Lass uns beginnen‘:
Polynomfunktionen
Winkelfunktionen
Übungsaufgaben
|
|
2.4 Weitere Übungen zu den Ableitungsregeln (freiwillig)
|

 

|
 Im Grunde hast die hier dieselbe Aufgabe, wie bei den ersten beiden Übungen, jedoch
sind diese Aufgaben etwas kniffliger.
Viel Erfolg!
‘Nun, denn Reisender. Lass uns beginnen‘:
Exponential- & Logarithmusfunktionen
Im Grunde hast die hier dieselbe Aufgabe, wie bei den ersten beiden Übungen, jedoch
sind diese Aufgaben etwas kniffliger.
Viel Erfolg!
‘Nun, denn Reisender. Lass uns beginnen‘:
Exponential- & Logarithmusfunktionen
Übungsaufgaben
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



